A Multi-Type Multi-Span Network forReading Comprehension that Requires Discrete Reasoning

论文：https://arxiv.org/abs/1908.05514

代码：https://github.com/huminghao16/MTMSN

复现：https://github.com/Asimok/DROP

由于学校VPN暂时禁用，无法继续做实验，复现的实验只做了2/3

任务

​ 在QA场景中，当答案涉及各种类型，或离散（多个span为正确答案）时，模型需要更高的推理能力，本文提出了多类型多跨度网络（MTMSN），包含多种答案类型（如跨度、计数、否定和算术表达）的多类型答案预测器，与一个动态产生一个或多个span的多跨度提取模块。

​ 此外，还提出了一种算术表达式重排机制，对表达式候选者进行排序，以进一步确认预测结果。

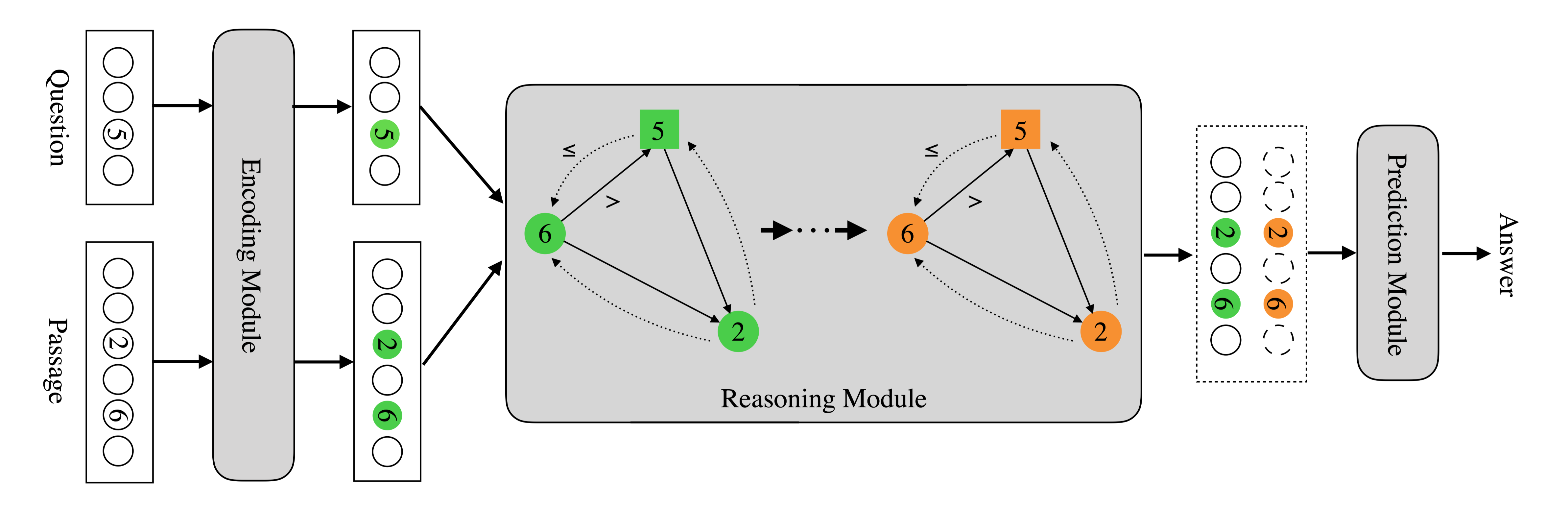
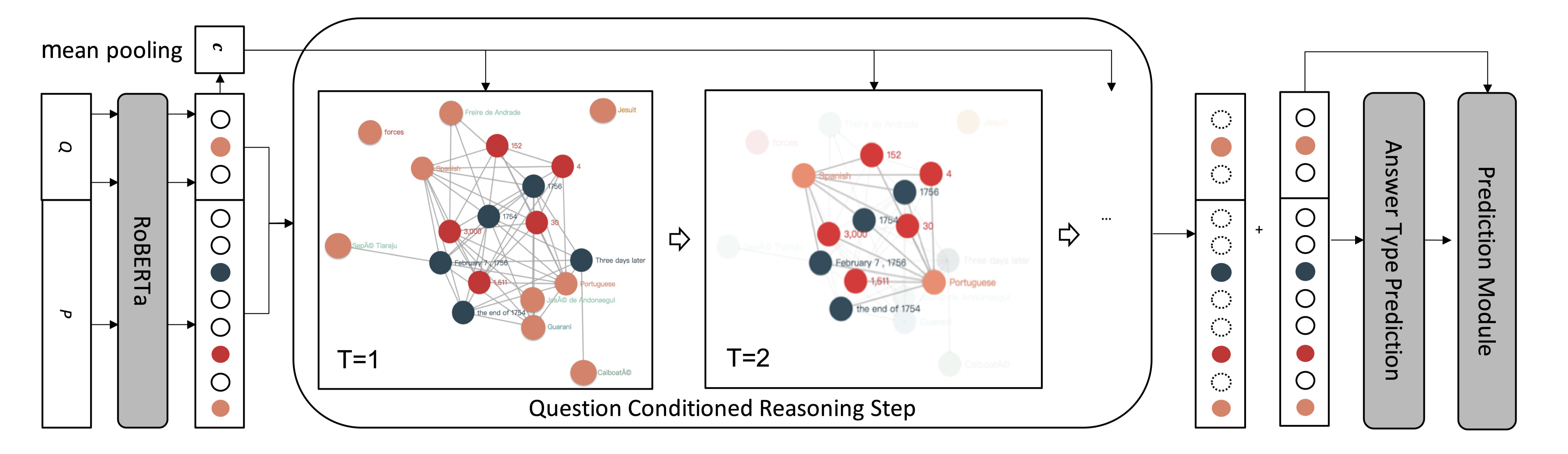
方法（模型）

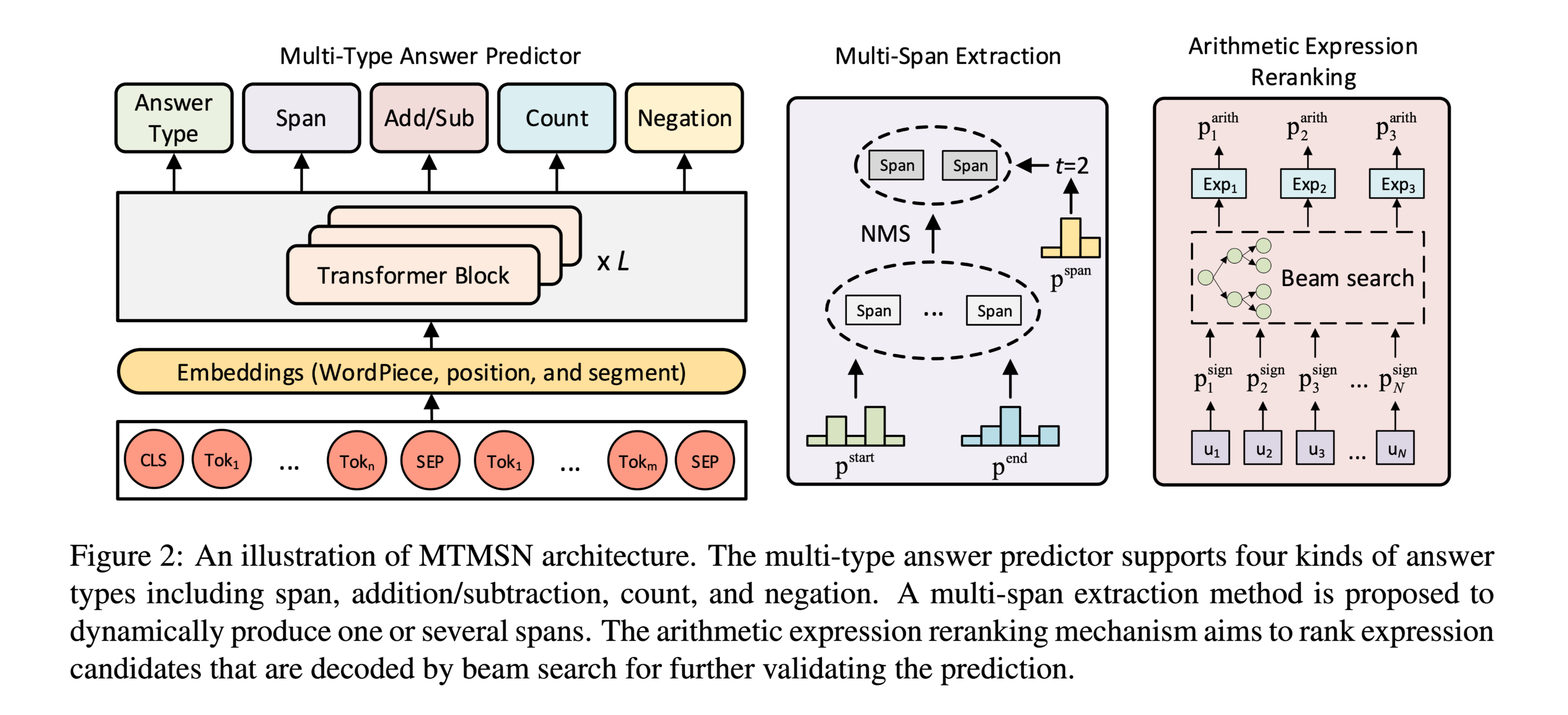
使用BERT做解码器，使用Transformer Block将word embedding映射到contextual enmbedding。

预测4种答案类型：

(1) span from the text; (2) arithmetic expression; (3) count number; (4) negation on numbers

模型首先根据passage-question pair预测答案类型，在根据不同答案类型做对应的答案预测。

对于multispan extraction模型可以预测出答案span的数量。

对于算数类问题，不直接使用最大概率的算数表达式，而是通过beam search对候选表达式重排序后确认预测答案。

模型在弱监督信号下训练，使所有可能的注释的边际似然函数概率最大化。

输入序列：[CLS] token, the tokenized question, a [SEP] token, the tokenized passage, and a final [SEP] token.

embeddings：

$$H_i= TransformerBlock(H_i−1)$$

Multi-Type Answer Predictor

直接从输入序列(question + passage)中提取答案片段。

与QANet model类似，使用最后4个block作为上下文表示，M0, M1, M2, M3。

Answer type prediction

分割$M_2$，作为$Q_2$和$P_2$的上下文表示：

$$α^Q= softmax(W^QQ_2) \\ h^Q_2= α^QQ_2$$

$P_2$的表示方法类似。

$$p^{type}= softmax(FFN([h^Q_2; h^P_2; h^{CLS}]))$$

$h^{CLS}$是最后一层的第一个向量。

FFN：feed-forward network，激活函数：GeLU

GeLU activation：

$$GELU(x)=xΦ(x)$$

其中$Φ(x) $是标准正态分布

这么选择是因为神经元的输入趋向于正态分布，使得当输入x减小的时候，输入会有一个更高的概率被dropout掉，这样的激活变换就会随机依赖于输入了。

Span

为了在不同layer的问题表述中总结问题信息，使用3个向量，$g^{Q_0}, g^{Q_1}, g^{Q_2}$，计算过程如下：

$$β^Q= softmax(FFN(Q_2) \\g^Q_2= β^QQ_2$$

$g^{Q_0}, g^{Q_1}$计算过程类似。

计算token作为开始和结束位置的概率。

Arithmetic expression

处理 (plus, minus, or zero)三种运算。

拼接$M_2,M_3$得到文章中出现数字的上下文表示：

$$U = (u_1, ..., u_N)$$

文章中出现N个数字。

计算每个位置的sign（plus, minus or zero）:

$$p^{sign}_i = softmax(FFN([u_i; h^{Q_2}; h^{P_2}; h^{CLS}]))$$

实质上仍然是一个分类问题，sign=0猜测，该位置的数字对表达式不起作用。

Count

仍然是一个多分类问题，$h_U$为文章中出现的所有数字的summarizes。-

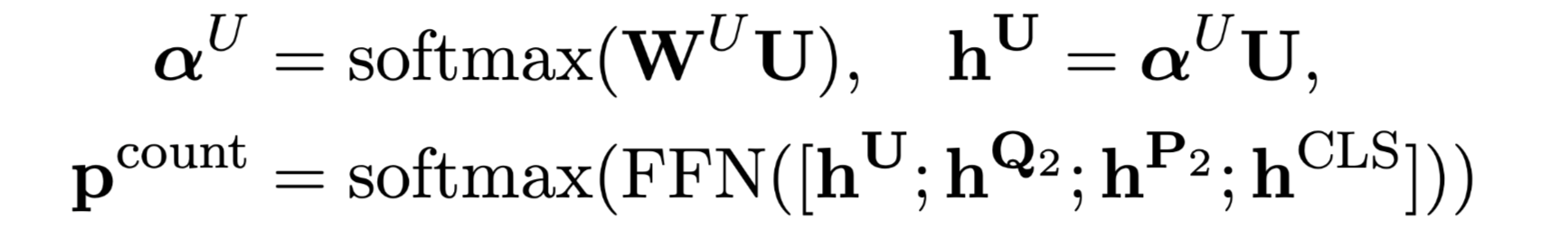
Negation

第i个数字是否作为否定句处理：

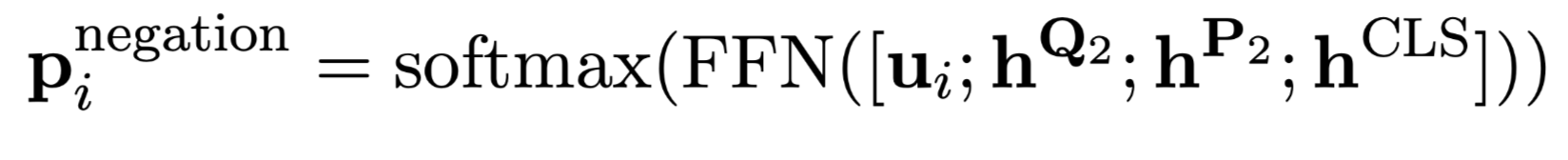
Multi-Span Extraction

处理multi-span情况时，转换为预测span的数量，可以看做一个多分类问题。

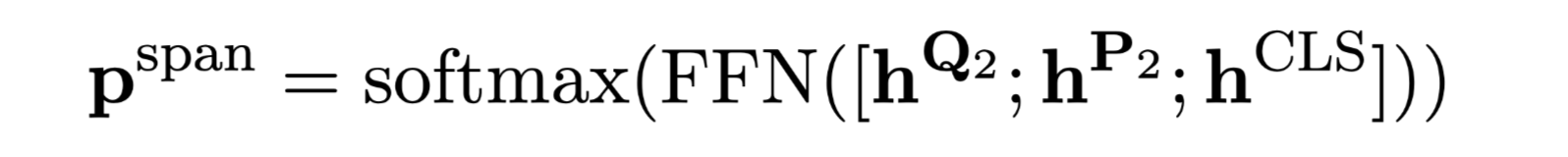
为得到无重叠的span，使用non-maximum suppression (NMS) 算法,重叠率计算使用 text-level F1 function.

具体来说，通过计算$p^{start}_k,p^{end}l$得到$span (k, l)$，按概率降序排序后，按概率从原始集合中迁移到新的集合，重复操作至原始集合为空，或者新集合已达到超参数限制的span最大数量，在此过程中，要将重叠的span去除。

Arithmetic Expression Reranking

由于表达式本身是数字的粗粒度语义信息，并没有结合上下文信息，因此会导致错误的表达式，具有最大概率的sign是负数或零，导致大的负值。

为解决这个问题使用beam search来产生排名靠前的算术表达式进行重排序。

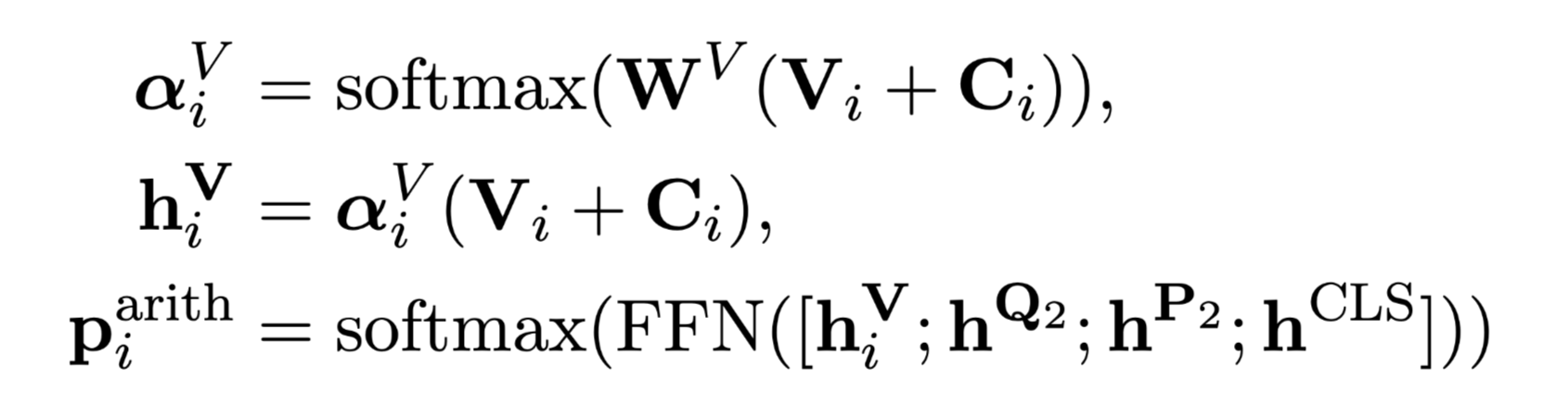
number vectors $V_i$

sign embeddings $C_i$

数据集

Drop数据集QA根据答案类型分类：

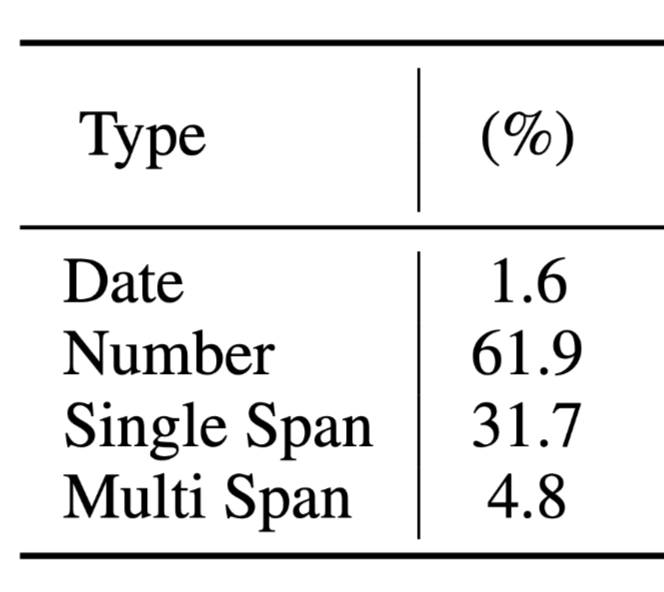
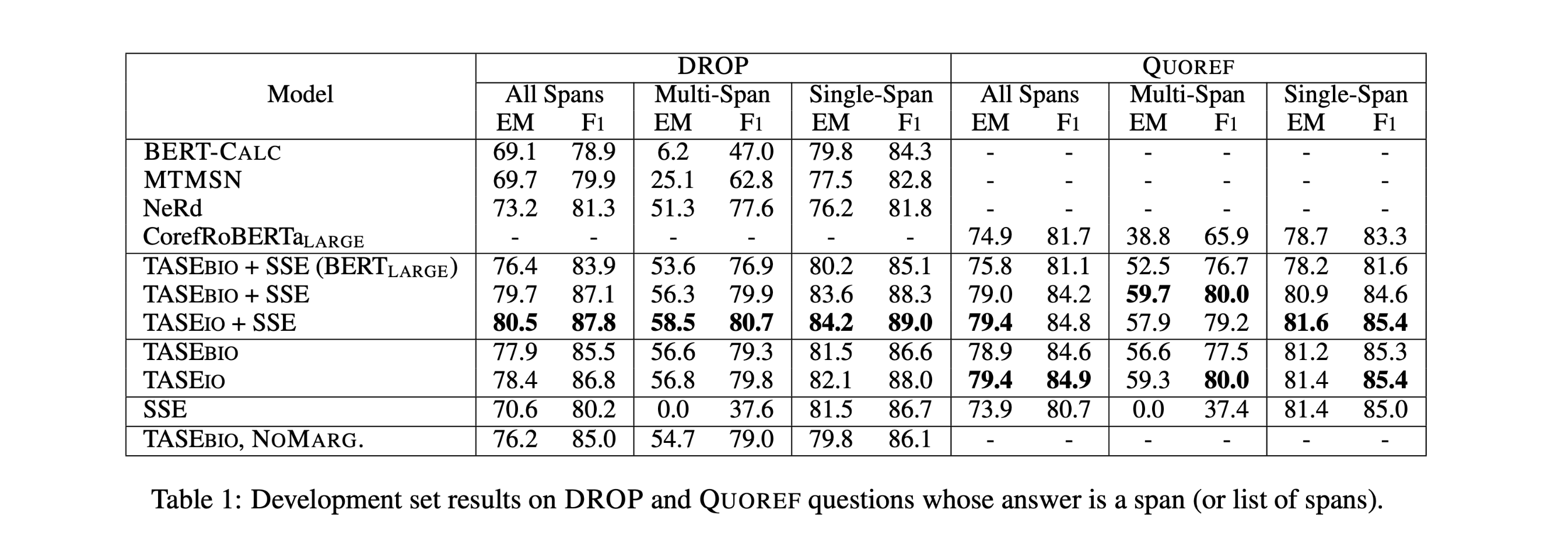
性能水平

实验结果：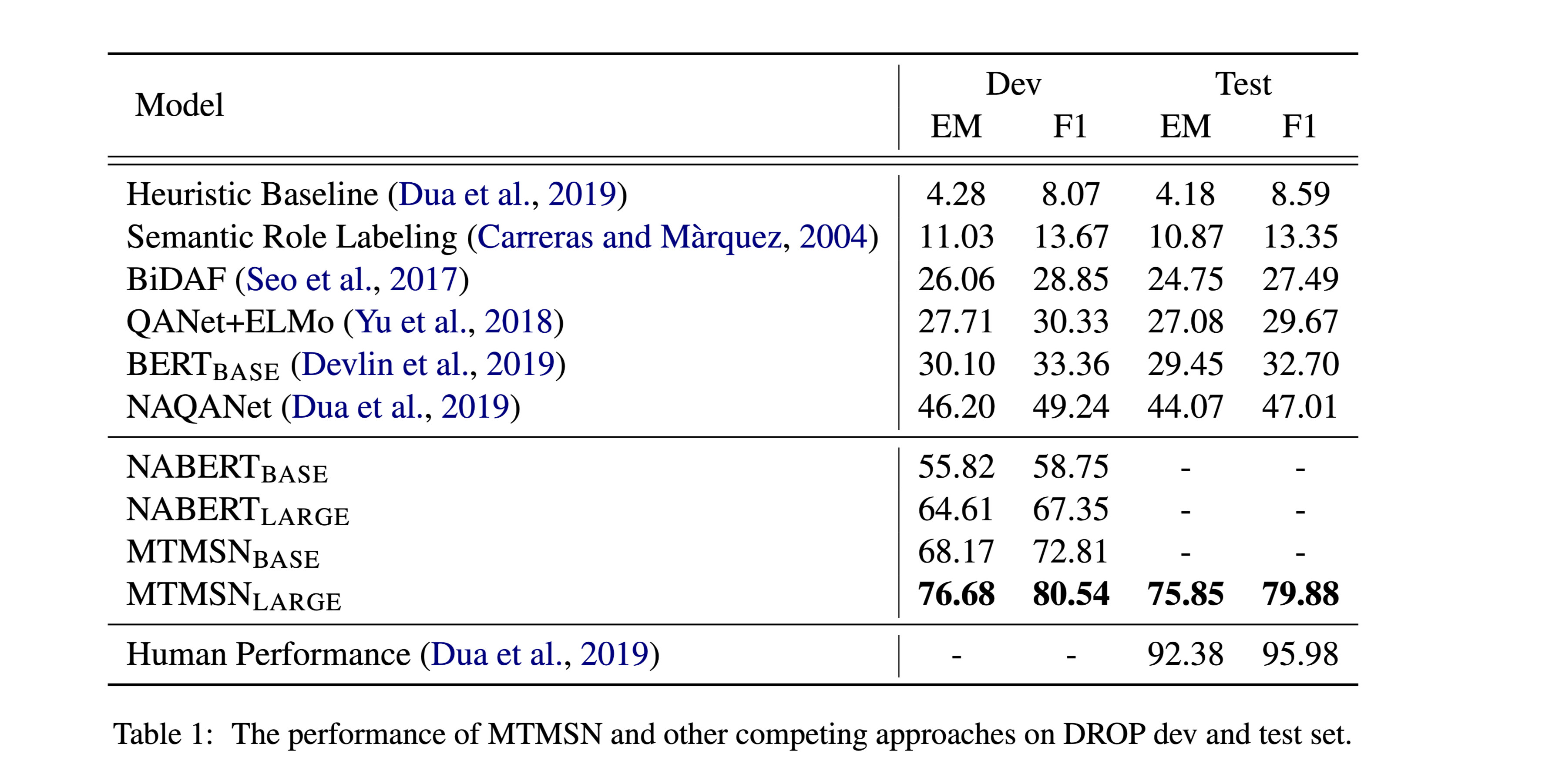

消融实验：

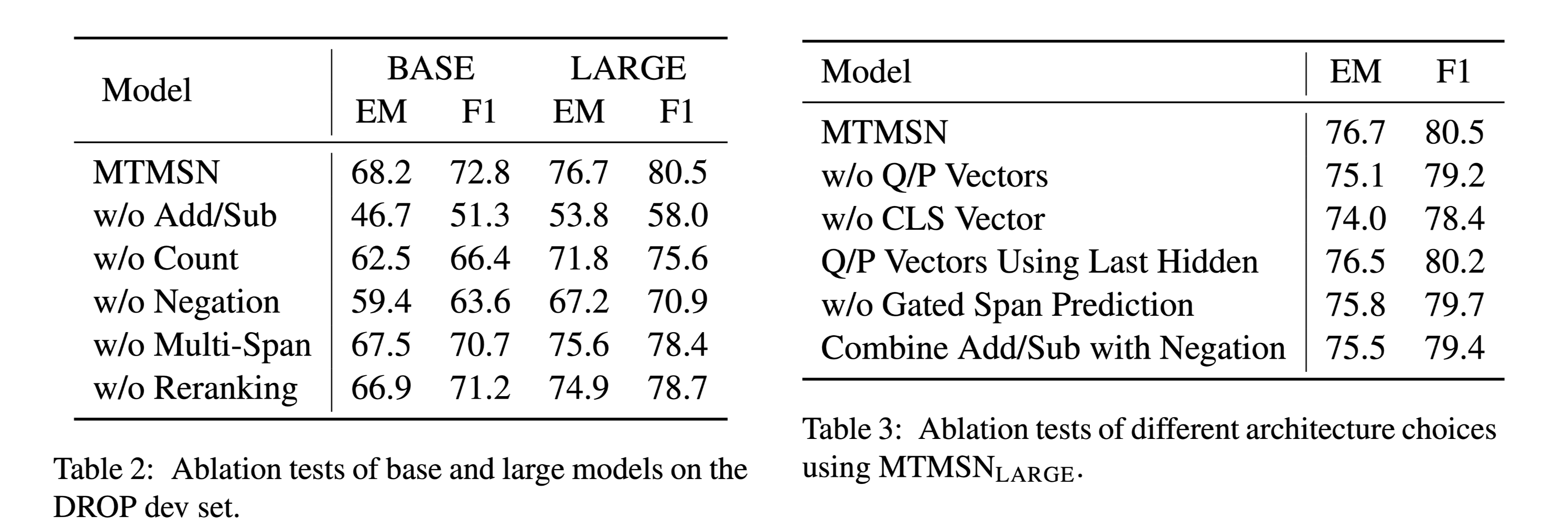
结论

MTMSN，是一个用于阅读理解的多类型多跨度网络，需要对段落内容进行离散推理。
使用多类型的答案预测器以处理否定句类型的问题，提出了一个多跨度的提取方法以产生多个答案，并设计了一个算术表达式重排机制以进一步确认预测结果。

该模型主要实现了复杂的数字推理。