Question Directed Graph Attention Network for Numerical Reasoning over Text
Question Directed Graph Attention Network for Numerical Reasoning over Text
论文:https://arxiv.org/abs/2009.07448
EMNLP2020
任务
对文本进行数字推理,如加法、减法、排序和计数,是一项具有挑战性的机器阅读理解任务,因为它需要自然语言理解和算术计算。为了应对这一挑战,本文提出了一种异构图表示,用于这种推理所需的文章和问题的上下文,并设计了一个问题导向图注意网络来驱动该上下文图上的多步数值推理。
方法(模型)
本文认为QANET和NumNet对于复杂的数值推理是不够的,因为它们缺少数值推理的两个关键要素:
- Number Type and Entity Mention:NumNet中的数字比较图无法识别不同的数字类型,缺少文档中提到的连接数字节点的实体信息。
- Direct Interaction with Question:NumNet中的图推理模块忽略了直接的问题表示形式,这在定位问题所指向的重要数字作为数字推理的枢纽时可能会遇到困难。
数字和实体之间的关联是学习数字推理模型的一个强有力的正则化:数字之间的比较和加/减法通常适用于那些具有相同类型或指代相同实体的数字。举两个例子:

其中有不同类型的实体和数字。两者都用不同的颜色强调:实体(黄色)、数字(红色)、百分比(蓝色)、日期(深蓝)、序数(蓝绿)。本文明确地将类型信息编码到模型中,并利用问题表示来进行推理过程。可以看到,第一段由5个”people counting“类型的数字,当给定数字类型时,如果模型学习提取以这个“population”问题为条件的“people counting”,推理难度将大大降低。
此外,图表中的实体提供了关于文章和问题之间相关性的明确信息。问题中的实体可能出现在文章中的几个句子中,表明每个数字如何通过这些桥接实体彼此关联,这有助于QA模型更好地收集和汇总信息以进行数字推理。 此外还可以观察到,当问题实体同时出现在一个句子中(第一段的最后一个句子)时,这可能暗示答案可以从该句子中得出。 第二个示例说明了跨度提取中的情况。 同样,当数字和“ Stephen Gostkowski”之间的相关关系明确时,该模型也会受益。
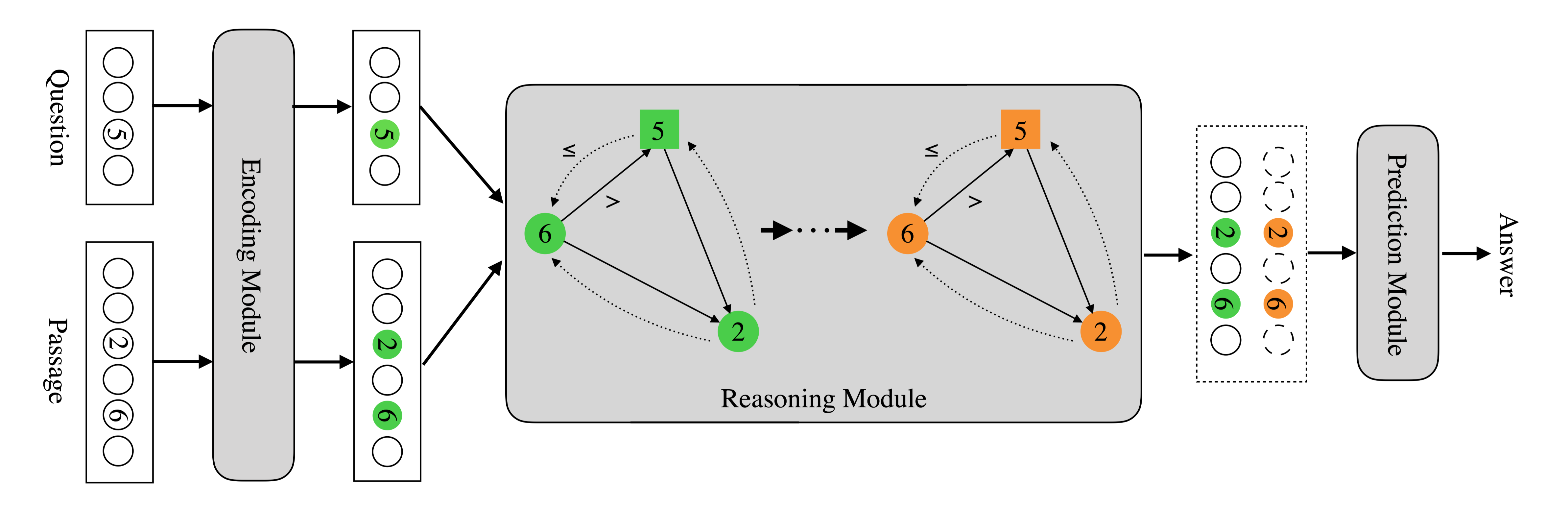
为了明确地将类型和实体信息集成到模型中,本文构建了一个异构有向图(下图,对应上表),其中节点由实体和不同类型的数字组成,而边可以编码不同类型的关系。图的节点由问题和文章中的实体和数字组成。同一类型的数字彼此紧密相连。一个句子中共同出现的数字和实体也是相互联系的。
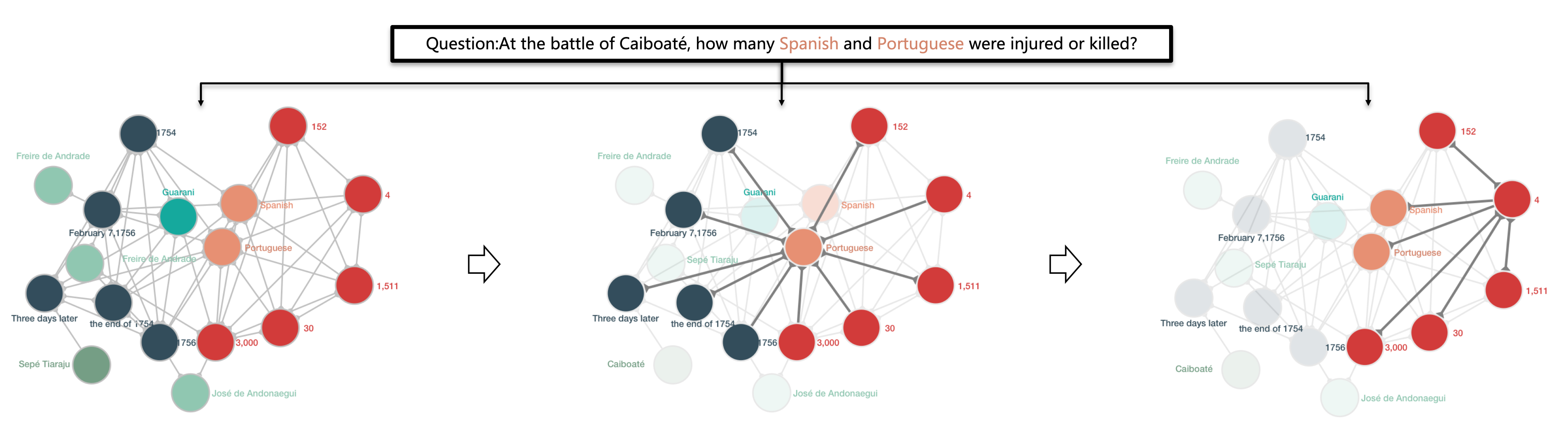
红色节点是数字,深蓝色节点是日期,其他节点是实体。边编码数字和实体之间的关系:具有相同数字类型(例如日期)的数字被连接在一起。该图将数字和同一个句子中的实体连接起来,以表示它们的同现。
在step-1中,模型关注包含Spanish 和 Portuguese实体的子图,因为它们在问题中被提及。在更新中,模型学习区分数字和日期,并提取与问题相关的数字。在step-2中,数字的表示由来自实体的消息以及进行推理的问题来更新。
基于这种异构图,本文提出了一种问题导向图注意网络(QDGA T),用于数值型MRC任务。由于与答案相关的数字可以由问题来引导,QDGAT在图推理过程中结合了问题的上下文编码。更具体地说,QDGAT使用上下文编码器,例如BERT和RoBERTa ,来提取问题和段落中的数字和实体的表示,作为图中每个节点的初始嵌入。通过异构图,QDGAT学会从以问题为条件的图中收集信息,用于数值推理。每个节点也由基于问题的上下文感知表示来描述,并且节点的表示通过消息传递迭代来更新。在用图神经网络进行多次消息传递迭代后,QDGAT逐渐聚合节点信息来回答问题。从这个意义上说,QDGAT以一种更符合人类感知和推理的方式抽象了段落和问题的表示,使模型产生了一种更可解释的推理模式。
Method
Problem Definition
在MRC任务中,每个数据样本由一个段落 $P$ 和一个相关的问题 $Q$ 组成。MRC模型的目标是根据 $P$ 回答问题 $Q$ ,给出答案 $A$ 。除了像标准MRC任务一样预测文本跨度之外,在数字推理的情况下,答案 $A$ 也可以是从算术计算(如排序、计数、加法和减法)中导出的数字。
Overall Framework
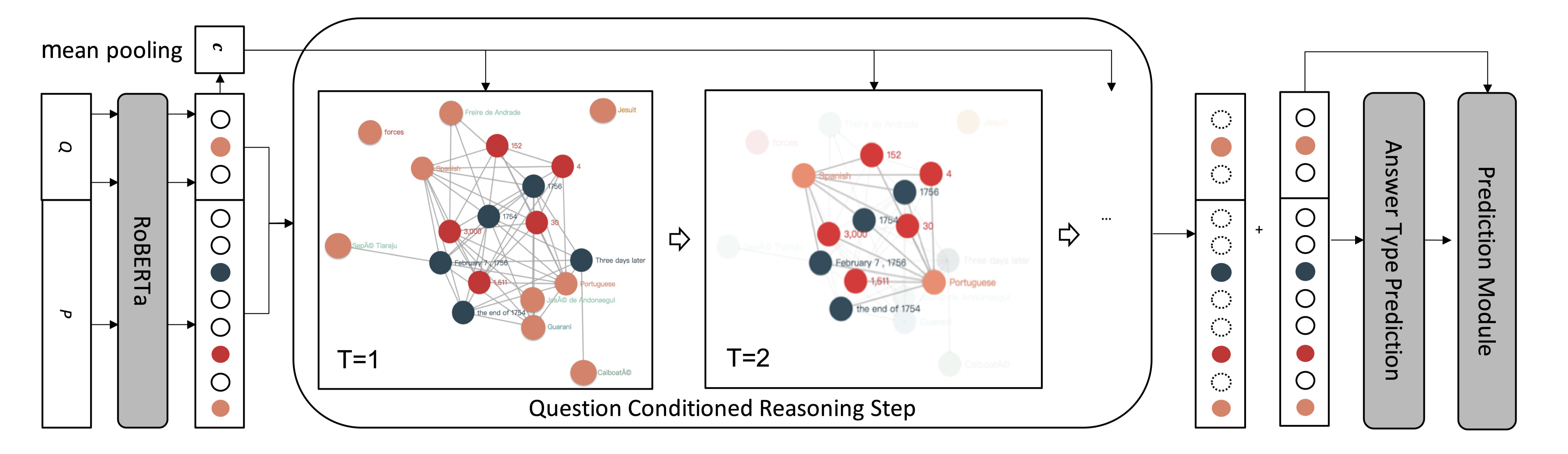
该模型由三个主要组件组成,representation extractor module, reasoning module, prediction module。representation extractor 负责语义理解。在extractor上,构造了一个具有类型化数字和相关实体的异构图。
Word Representation Extractor
RoBERTa处理passage和question,输入形式[CLS] Q [SEP] P [SEP]串联:

Graph Construction
该模块从文本数据构建异构类型的图形。图 $G=(V,E)$包含数字 $N$和实体 $T$,两者都由外部命名实体识别系统(CoreNLP)识别,节点 $V = {undefined N ,T}$,其边 $E$ 编码数字类型的信息和数字与实体的关系。
具体来说,NER将文本中的每个token标记为21个预定义类别之一。标记为NUMBER, PERCENT, MONEY, TIME, DATE, DURATION, ORDINAL 的被视为数字。此外,本文增加了一个额外的标记YARD并且利用了一个数字提取器去提取剩余的数字,它们也被标记为NUMBER。
数字提取器word2num:https://pypi.org/project/word2number/
所有这些标记用8种数字类型 $V_N=(NUMBER,PERCENT,MONEY,TIME,DATE, DURATION,ORDINAL,YARD)$构成数字集 $N$。至于其他已识别的标记,将它们映射到标签ENTIT_Y中,以构建类型集为 $V_T = {undefined \ ENTIT_Y }$的实体集 $T$,来表示节点的类型。类型信息可以直接通知模型找到与问题相关的数字,从而降低推理难度。边$E$编码数字和实体之间的关系,对应两种情况。
- The edge between the numbers
- The edge between the entity and the number
第一种情况的边将相同类型的数字聚集在一起,这提供了一个明显的线索来帮助对这些数字进行推理。在第二种边大致表示数字和实体之间的相关性。总的来说,该图有9个关系$R$,即8个数字类型关系和1个ENT+DIGIT关系。
Numerical Reasoning Module
数字推理模块,即QDGAT,建立在表示和图提取器的基础上。基于图 $G=(V,E)$,QDGAT网络可以表示为:
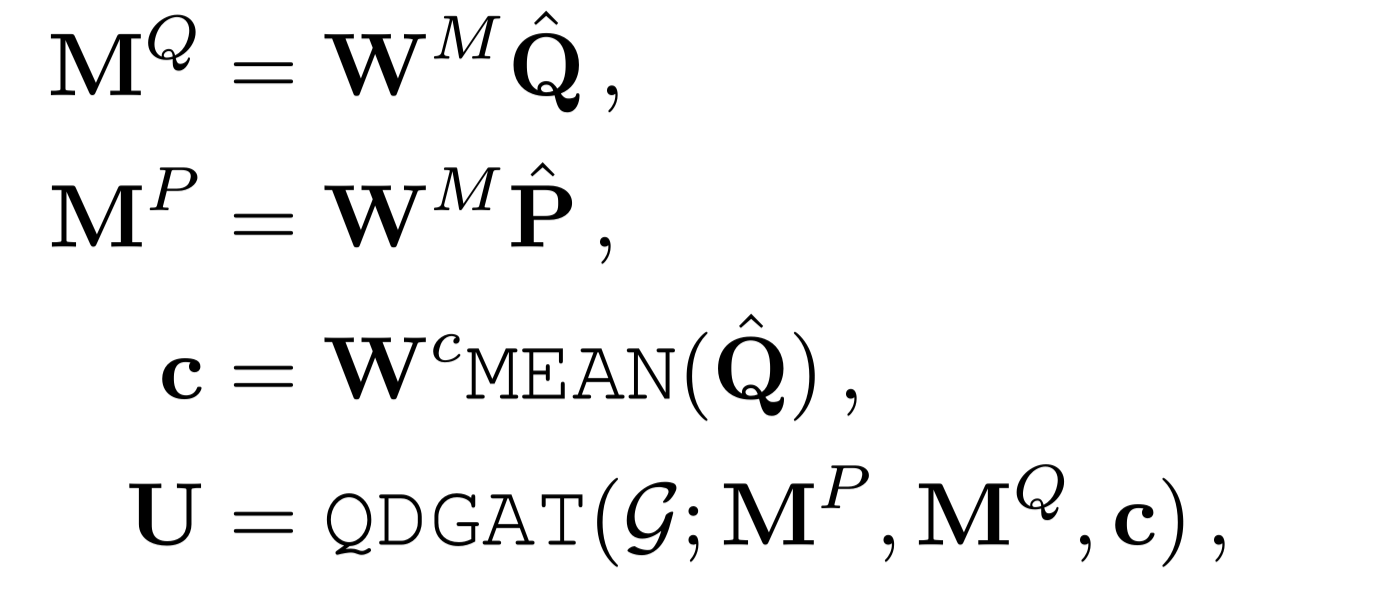
$W^M$是投影矩阵
$MEAN$表示为mean pooling
$W^c$投影问题表示的平均向量以导出$c$$c$是用于指导QDGAT中推理的问题语言嵌入
QDGAT然后对表示$M^P \ M^Q$和以问题导向$c$为条件的图$G$进行推理
Prediction Module
预测模块将图推理网络$U$的输出作为最终预测。目前NAQANet和NumNet+中的答案类型一般分为三类:
- 跨度提取
- 计数
- 算术表达式
本文为这些答案类型实现了单独的模块,它们都以图网络$U$和问题嵌入$c$的输出作为输入。具体如下:
- 跨度提取:有三个跨度提取任务,即单篇文章跨度、多篇文章跨度、单问题跨度。单个跨度提取的概率是由问题或段落中开始和结束位置的概率的乘积导出的。
- 计数:这个问题被认为是一个10类分类问题(0-9),它涵盖了DROP数据集中大约97%的计数问题。
- 算术表达式:答案由一个算数表达式给出,在DROP数据集中,只涉及加法和减法运算。本文通过将每个数字分类为(1,0,+1)中的一个来实现这一点,然后将其用作数值表达式中数字的系数,以得出最终答案。
本文使用一个独特的分类网络将数据样本分类为五种细粒度类型$T$之一。每个类型求解器使用一个唯一的输出层来计算条件答案概率 $p(A|T)$。
Question Directed Graph Attention Network
基于异构图$G$,QDGAT对问题进行上下文感知的数值推理,通过在数字和实体之间传递消息的多次迭代来收集关系信息。它通过图中的边动态地确定与哪些对象交互,并通过图发送消息来传播关系信息。为了实现这一点,用上下文化的问题表示来扩充推理模块。例如,在表1的例子中,任务是找出有多少西班牙人和葡萄牙人受伤或死亡。实体和数字被显式标记,并在异构图中建模,如图1所示。QDGAT能够提取相关的实体,即西班牙语和葡萄牙语,条件是 $c$。在与这两个实体相关的数字中,其中一些是日期类型的,而其他的是关于人的。但是,应该只关注问题所要求的与人有关的数字。然后,模型对这些数字进行推理,得出答案计算的表达式。
数据集
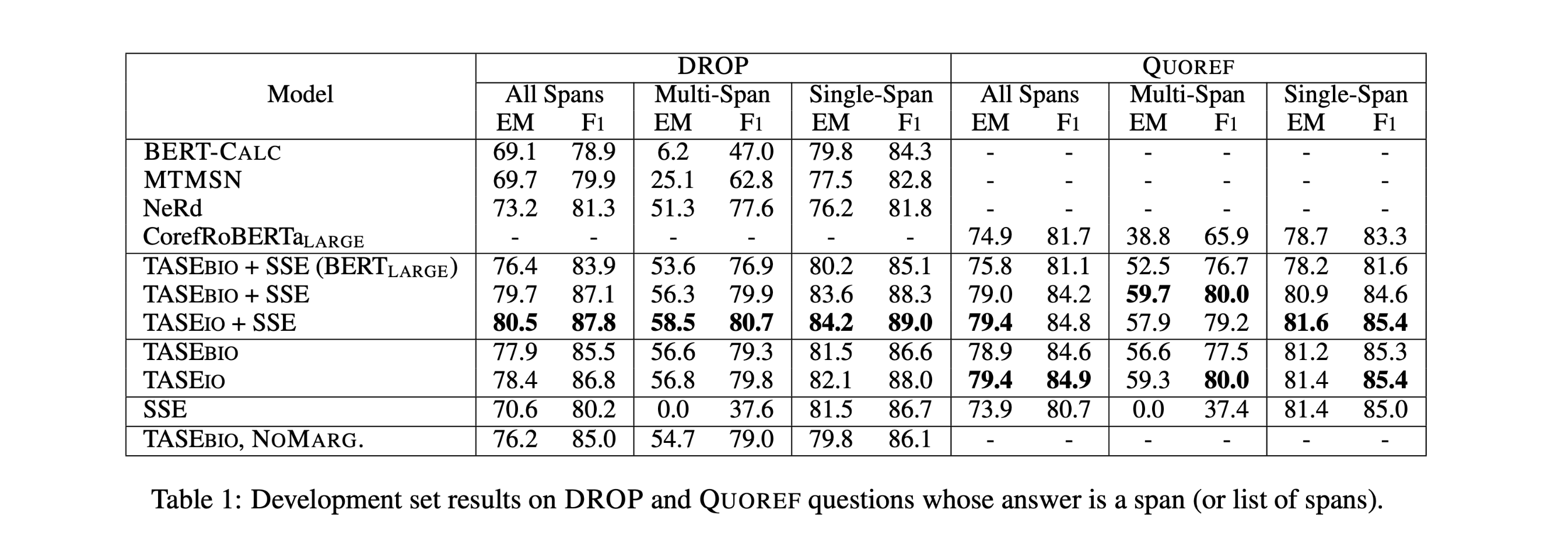
DROP:DROP是通过在维基百科的段落上众包问答对来构建的,在最初的train/dev/test部分包含/ 9536 / 9622个样本。使用精确匹配(EM)和F1分数作为评估指标。
性能水平
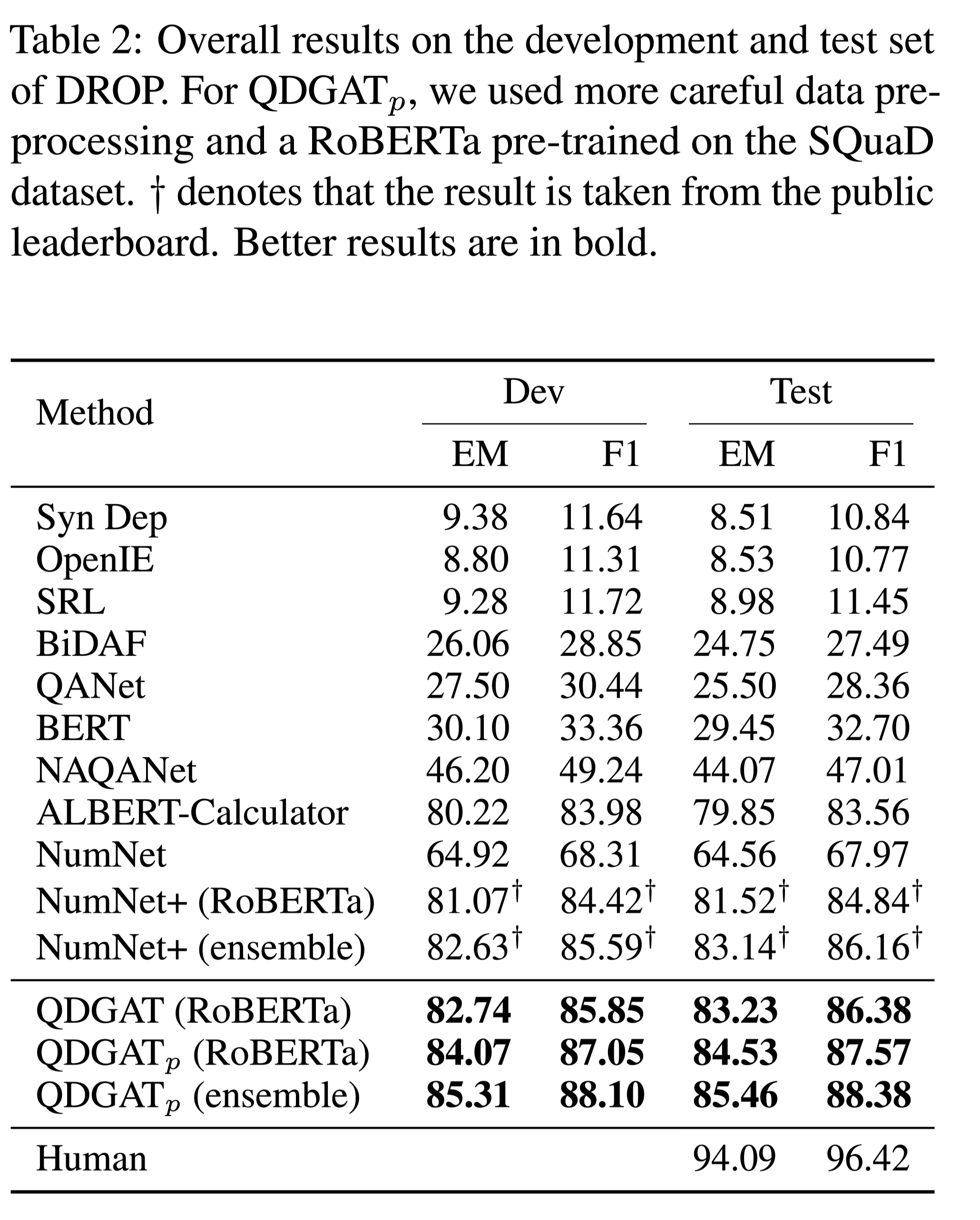
结论
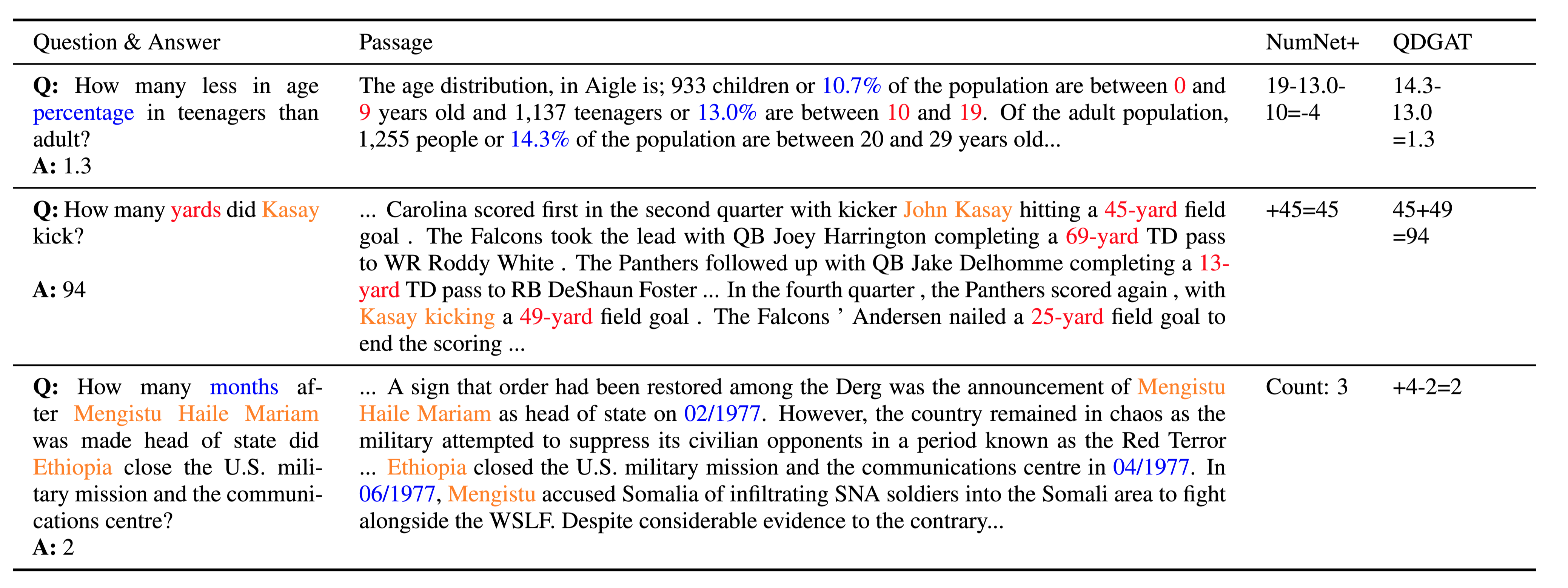
QDGAT在与数字和日期相关的问题上工作得更好,与span提取相比,这需要更具体的数字推理。
在这项工作中,本文提出了一种名为QDGAT的新型方法,用于机器阅读理解任务中的数字推理。我们的方法不仅建立了一个包含不同类型的数字、实体和关系的更紧凑的图,可以作为其他复杂推理任务的通用方法,而且还将推理的条件直接放在问题语言嵌入上,通过图和被迭代传递的改变信息来调节注意力,实现推理。
case study