没有胡子的猫Asimok

使用Numpy实现机器学习表达式：$y=3x^2+2$ 模型：$y=wx^2+b$ 损失函数：$Loss=\frac{1}{2}\sum_{i=1}^{100}(wx^2_i+b-y_i)^2$ 对损失函数求导：$\frac{\partial Loss}{\partial w}=\sum_{i=1}^{100}(wx^2_i+b-y_i)^2x^2_i$ $\frac{\partial Loss}{\partial b}=\sum_{i=1}^{100}(wx^2_i+b-y_i)^2$ 利用梯度下降法学习参数，学习率为:lr $w_1-=lr*\frac{\partial Loss}{\partial w}$ $b_1-=lr*\frac{\partial Loss}{\partial b}$ 12import numpy as npfrom matplotlib import pyplot as plt 1.生成训练数据123456#设置随机种子，生成同一份数据np.random.seed(100)x = np.linspace(-1, 1, 100).reshape(100, 1 ...

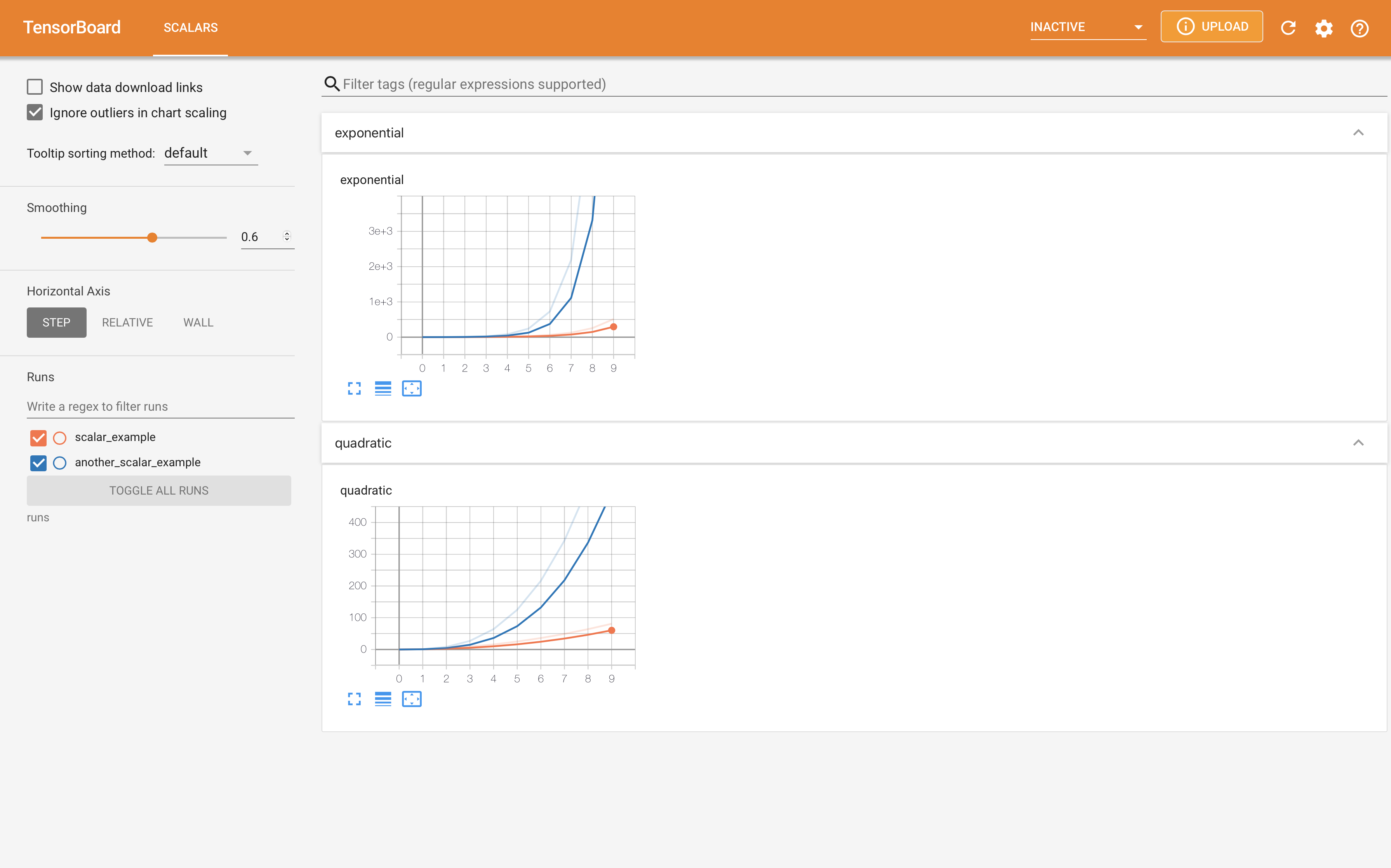
用tensorboardX可视化神经网络安装：pip install tensorboardX 12345from tensorboardX import SummaryWriterwriter = SummaryWriter('runs/scalar_example')for i in range(10): writer.add_scalar('quadratic', i**2, global_step=i) writer.add_scalar('exponential', 2**i, global_step=i) 12345writer = SummaryWriter('runs/another_scalar_example')for i in range(10): writer.add_scalar('quadratic', i**3, global_step=i) writer.add_scalar('exponential', 3** ...

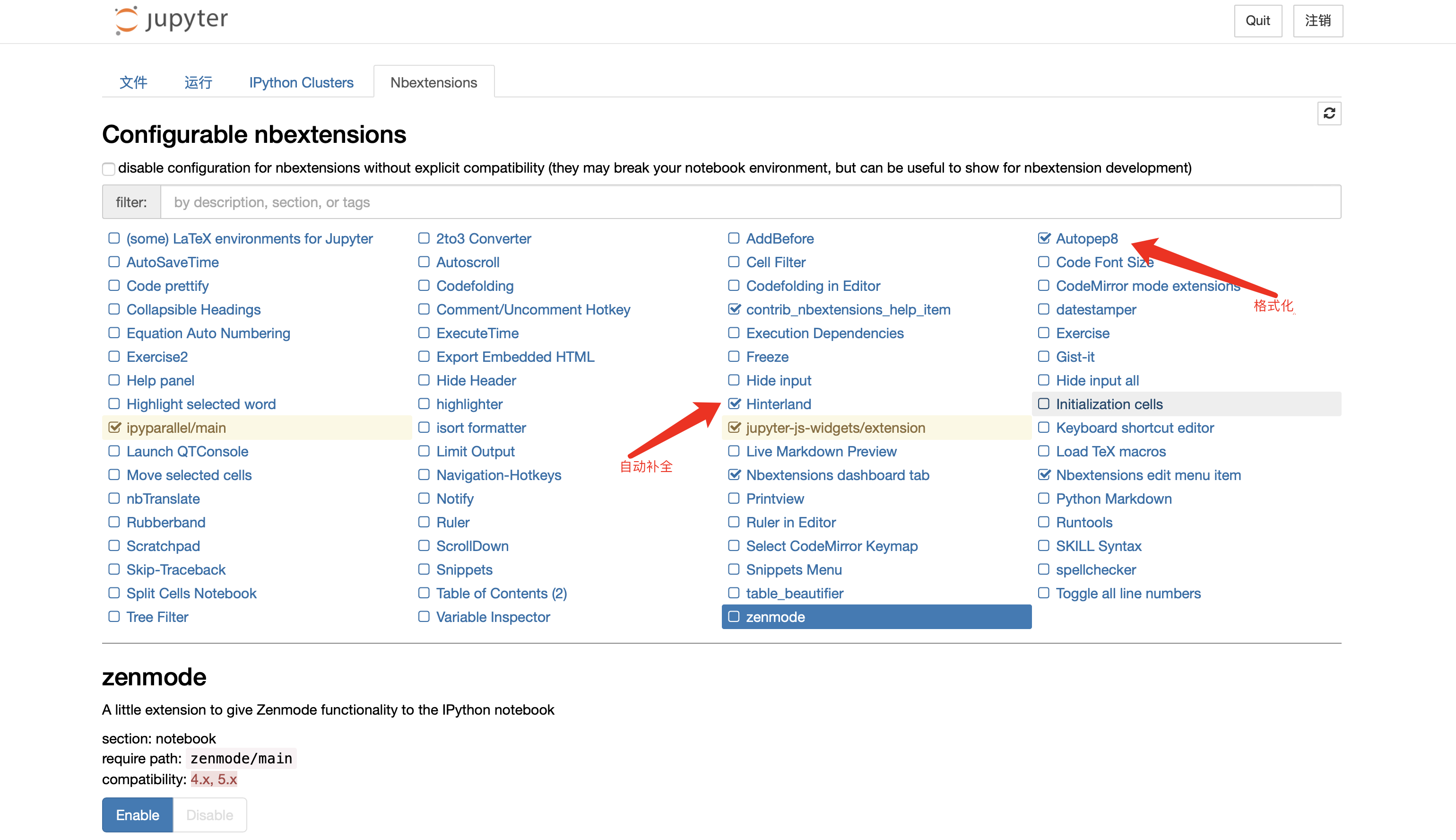
Jupyter Notebook 实现代码提示自动补全和代码格式化安装插件nbextensions1.安装jupyter_contrib_nbextensionspip install --user jupyter_contrib_nbextensions -i https://pypi.mirrors.ustc.edu.cn/simple jupyter contrib nbextension install --user 2.安装nbextensions_configuratorpip install --user jupyter_nbextensions_configuratorjupyter nbextensions_configurator enable --user 如果出错提示“Exception: Jupyter command jupyter-contrib not found.” 则使用conda强制安装，conda install -c conda-forge jupyter_nbextensions_configurator 配置

Jupyter Notebook 实现代码提示自动补全和代码格式化安装插件nbextensions1.安装jupyter_contrib_nbextensionspip install --user jupyter_contrib_nbextensions -i https://pypi.mirrors.ustc.edu.cn/simple jupyter contrib nbextension install --user 2.安装nbextensions_configuratorpip install --user jupyter_nbextensions_configuratorjupyter nbextensions_configurator enable --user 如果出错提示“Exception: Jupyter command jupyter-contrib not found.” 则使用conda强制安装，conda install -c conda-forge jupyter_nbextensions_configurator 配置

HOLE Holographic Embeddings of Knowledge Graphs 基于向量的循环相关 任务 提出全息嵌入(holographic embeddings，HOLE)来学习整个知识图的组成向量空间表示。 在组合向量空间模型的框架内研究从知识图谱学习的问题。 方法（模型）compositional vector space models 组合向量空间模型 Pr(\phi_p(s,o)=1|\Theta)=\sigma(\eta_{spo})=\sigma(\mathbf{r}_p^T(\mathbf{e}_s◦\mathbf{e}_o)) \phi_p(s,o)：特征函数 ◦ ：复合算子，从嵌入$\mathbf{e}_s$，$\mathbf{e}_o$创建$（s，o）$的复合向量表示。 通过最大限度地减少（正则化）logistic损失来实现最好地解释数据集的实体和关系的表示。 \min\sum_{i=1}^mlog(1+exp(-y_i\eta_i))+\lambda||\Theta||_2^2 对于关系数据，最小化 logistic 损失具有额 ...

标量反向传播 当目标张量为标量时，backward()无需传入参数。 例子：假设$w,x,b$都是标量，$z=wx+b$ ，对标量$z$调用backward()方法。 自动求导的主要步骤1import torch 1.定义叶子结点，算子节点 如果需要对Tensor求导，requires_grad要设置为True。 123456789101112# 定义输入张量xx = torch.Tensor([2])# 初始化权重参数w,偏置b,#设置requires_grad为True，使用自动求导w = torch.randn(1,requires_grad=True)b = torch.randn(1,requires_grad=True)# 设置前向传播y = torch.mul(w,x)z = torch.add(y,b)# 查看requires_grad属性print(x.requires_grad)print(y.requires_grad)# 因为与w,b具有y依赖关系，所以x,y的requires_grad也是True。 False True 2.查看叶子结点，非叶子结点的 ...

TransE 《Translating Embeddings for Modeling Multi-relational Data》 任务 在低维向量空间中，将多种关系的图谱中的实体和关系在一个低维空间中进行表示，获得每个实体的表征结果。 提出一种易于训练的规范模型，该模型包含数量较少的参数，并且可以扩展到非常大的知识库。 对知识图谱中的多元关系数据进行建模，在不引入额外知识的情况下，高效的实现知识补全，关系预测。 方法（模型）TransE：基于能量的模型，用于学习实体的低维嵌入。 关系作为向量空间转变的桥梁：如果三元组(h,l,t)成立，则头实体embedding和关系embedding相加约等于尾实体的embedding。 $h+l ≈ t$ 利用空间传递不变形，找到一个实体和向量空间，使得整关系三元组之间的势能差值最小。 $min(t − ( h + l ))$ 模型 给定一个训练集 S ，三元组表示为 $( h , l , t )$，其中 $h , t ∈ E ,l ∈ L$ ，实体和关系的嵌入维度设为 k，希望 $h + l$ 与 $t$能够尽可能的 ...

请大家务必升级到1.0（正式版）及以后版本下载地址汇总 问题汇总 账号密码不正确教务系统升级改版，初次登陆请登录教务管理系统网页版重置密码。 验证码刷新不出来登录 jwgl.nepu.edu.cn 看看自己有没有因为访问次数过多禁止访问！等解禁就好啦！ （或者更换网络环境，更换ip） 绩点怎么变低了教务处更新了绩点计算规则！（大家都低了没关系/狗头）更新日式 v1.5正式版：2020.10.26中午 为方便大家计算综测，平均分计算中去除“公选”类型的课程。与智育成绩算法一致。v1.4正式版：2020.10.25晚上 优化页面交互逻辑 修改登录界面 修复已知bugv1.3正式版：2020.10.25早晨 新增官方课表 修改程序图标 修复其他已知bugv1.1正式版：2020.10.24下午 修复部分同学 全部学期 成绩查询失败的问题 修复其他已知bug v1.1正式版：2020.10.24凌晨 应用内陆续推送更新，本次为强制更新，v1.0版本在应用内更新后方可正常使用。 修复部分机型成绩查询失败的问题。 修复其他已知bug v1.0正式版：2020.10.23晚上 重大升级： 终 ...

1. 知识图谱(KG) 由实体(节点)和关系(不同类型的边)组成的多关系图。 每条边都表示为形式(头实体、关系、尾实体)的三个部分，也称为事实 1.1 问题 这类三元组的底层符号特性通常使KGs很难操作 1.2 解决： 提出了一种新的研究方向——知识图谱嵌入。 1.3 关键思想 嵌入KG的组件，包括将实体和关系转化为连续的向量空间，从而简化操作，同时保留KG的原有的结构。 2. 融合事实信息2.1 平移距离模型 平移距离模型利用了基于距离的评分函数，通过两个实体之间的距离对事实的合理性进行度量。 2.1.1 TransE模型 平移不变现象 TransE模型：将知识库中的关系看作实体间的某种平移向量。 对于每个事实三元组(h,r,t)，TransE模型将实体和关系表示为同一空间中，把关系向量r看作为头实体向量h和尾实体向量t之间的平移即 $h+r≈t$。 可以将r,看作从h到t的翻译 知识库中的实体关系类型可分为 一对一 、一对多 、 多对一 、多对多4 种类型，而复杂关系主要指的是 一对多 、 多对一 、多对多的 3 种关系类型。 优点 TransE模型的参数较 ...