算法笔记-算法&数据结构(更新中)
算法笔记-算法&数据结构
记录刷题过程中遇到的重要知识点和新知识!
算法&数据结构
二分
左闭右闭风格 [left,right]
``1
2
3
4
5while (left <= right) // 当left==right,区间[left, right]依然有效,所以用 <=
right = middle - 1; // target 在左区间,所以[left, middle - 1]
left = middle + 1; // target 在右区间,所以[middle + 1, right]找中间位置 靠右的元素
1 | mid = left + (right - left)/2; # 防止溢出 |
- 完整写法
1
2
3
4
5
6
7
8
9
10
11
12def search(self, nums: List[int], target: int) -> int:
# 二分查找
left, right = 0, len(nums) - 1
while left <= right:
middle = left + (right - left) // 2
if nums[middle] == target:
return middle
elif nums[middle] > target: # 在左区间
right = middle - 1
else:
left = middle + 1
return -1
bissect库
1 | def search(self, nums: List[int], target: int) -> int: |
以下为c++风格
upper_bound( begin,end,num):返回的是数值 第一个 出现的位置。从数组的begin位置到end-1位置二分查找第一个大于num的数字,找到返回该数字的地址,不存在则返回end。
通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
1
2
3
4int pos = upper_bound(times.begin(), times.end(), t) - times.begin() - 1;
// - 1 表示t应该插入的位置
// 不减1 代表边界下标
// 因为返回的地址是 第一个 大于t 的下标lower_bound( begin,end,num):返回的是数值 最后一个 出现的位置。从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字,找到返回该数字的地址,不存在则返回end。
通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
binary_search(起始地址,结束地址,要查找的数值) :返回的是是否存在这么一个数,是一个bool值。
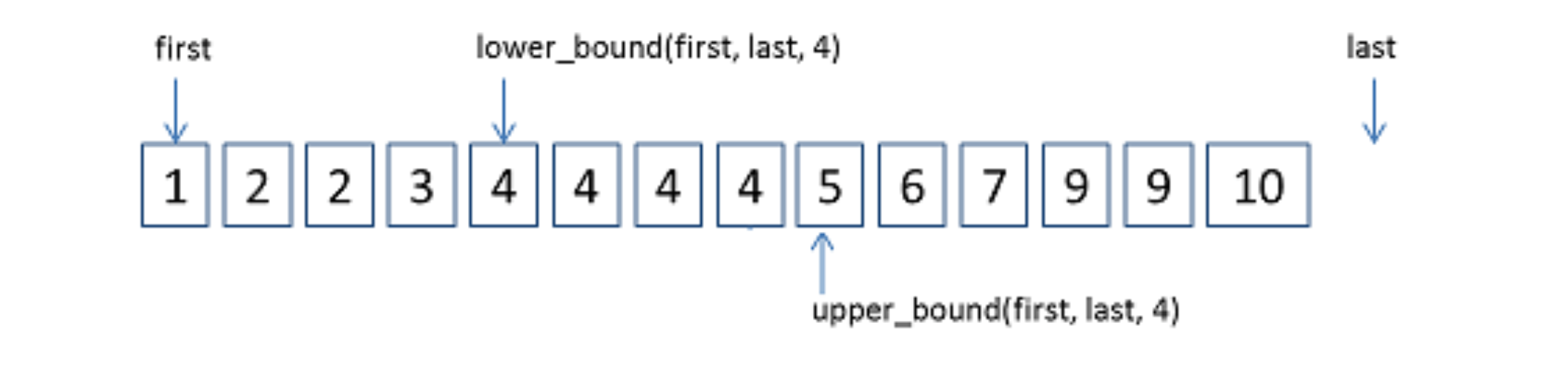
举例
x[a,b]是一个区间
1 | int l = lower_bound(pos.begin(), pos.end(), x[0]) - pos.begin(); // 第一次出现的位置 |
- 手写实现
- 中间节点为
int i = left + (right - left ) / 2;
if(count>=k) right=mid;
1 | int left =1,right=m*n; |
- 找到第一个小于目标值的位置
1 | int first_low(vector<int> num_list, int t) { |
- 最后一个大于目标值的位置 下一个位置可插入
1 | int first_low(vector<int> num_list, int t) { |
双指针
快慢指针
- 元素相对位置不变化
1
2
3
4
5
6
7
8
9
10def removeElement(self, nums: List[int], val: int) -> int:
# 双指针
slow = 0
n = len(nums)
#慢指针维护插入位置
for fast in range(n):
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
return slow
- 或者是a指针先移动n步,再与b指针同时移动
1
2
3while gap:
gap-=1
chain1=chain1.next
相向指针
- 相向双指针方法,基于元素顺序可以改变的题目描述改变了元素相对位置,确保了移动最少元素
- 相对位置可改变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16def removeElement(self, nums: List[int], val: int) -> int:
# 双向指针
left, right = 0, len(nums) - 1
while left <= right:
# 找到左边待插入位置
while left <= right and nums[left] != val:
left += 1
# 找到右边符合条件的位置
while left <= right and nums[right] == val:
right -= 1
# 交换元素
if left < right:
nums[left] = nums[right]
left += 1
right -= 1
return left
三数之和
15. 三数之和
关键思路:排序后使用三个指针 遍历n次,分别指向 i,i+1,len-1,通过和的情况控制指针的移动方向。
需要注意的是去重,如果当前元素已使用,并且后面存在连续的相同值,应该跳过,因为对于排序的数组而言,值相同意味着枚举的情况也相同。
与四数相加II不同的是,需要去重,使用哈希表对元组去重并不方便,因此考虑使用双指针。
关键代码:
集合去重:
- 至少遍历一次后再对集合去重,否则会丢失未枚举过的集合。
- 我们要求的是对集合去重,而不是去重集合中的元素,因此要写成nums[i] == nums[i - 1]的形式。
1
2
3# 避免重复 从值不相同的位置开始
if i > 0 and nums[i] == nums[i - 1]:
continue
1 | class Solution: |
- 四数之和也是类似的解法,只是在三数之和的基础上套了一层for循环,只需要注意去重条件和目标值就好了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
# 排序后使用双指针
ans = []
nums.sort()
for i in range(len(nums)):
# 剪枝
if nums[0] > target >= 0:
return []
# 避免重复 从第一个不重复的位置开始
if i > 0 and nums[i] == nums[i - 1]:
continue
for j in range(i + 1, len(nums)):
# 注意去重时间 要在遍历完至少一次后再去重,因为题目要求的是相同元素的集合去重 而不是限制去重相同元素
if j > i + 1 and nums[j] == nums[j - 1]:
continue
t = nums[i] + nums[j]
left = j + 1
right = len(nums) - 1
while left < right:
if t + nums[left] + nums[right] == target:
ans.append([nums[i], nums[j], nums[left], nums[right]])
# 去重
while left < right and nums[left] == nums[left + 1]:
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
left += 1
right -= 1
elif t + nums[left] + nums[right] > target:
right -= 1
else:
left += 1
return ans
滑动窗口
- 核心之处在于,控制窗口大小的动态变化
1
2
3
4for 右边界
while ...
# 左边界变化的逻辑写在while
左边界++ 如果数量或者种类有限制,缩放窗口时应该控制
在指定字符的情况下,我们可以计算其最大连续数目。具体地,我们使用滑动窗口的方法,从左到右枚举右端点,维护区间中另一种字符的数量为 sum,当 sum 超过 k,我们需要让左端点右移,直到 sum≤k。移动过程中,我们记录滑动窗口的最大长度,即为指定字符的最大连续数目。
1 | int maxConsecutiveChar(string& answerKey, int k, char ch) { |
求长度最小的子数组
209. 长度最小的子数组1
2
3
4
5
6
7
8
9
10
11
12
13def minSubArrayLen(self, target: int, nums: List[int]) -> int:
# 滑动窗口 一重循环 控制窗口的结束位置
i, sums = 0, 0
ans = len(nums) + 1
for j in range(len(nums)):
sums += nums[j]
# 判断是否可以缩放滑窗大小
while sums >= target:
cur_len = j - i + 1
ans = cur_len if cur_len < ans else ans
sums -= nums[i]
i += 1 # 更新区间
return ans if ans < len(nums) + 1 else 0
76. 最小覆盖子串1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26def minWindow(self, s: str, t: str) -> str:
n = s.__len__()
cnt = {k: 0 for k in t}
need = Counter(t)
i = 0
gap = n + 1
valid = 0
res = ''
for j in range(n):
if s[j] in cnt:
cnt[s[j]] += 1
if need[s[j]] == cnt[s[j]]:
valid += 1
# 判断是否缩放区间
while valid == len(need):
if s[i] in cnt:
# 更新计数
if need[s[i]] == cnt[s[i]]:
valid -= 1
cnt[s[i]] -= 1
# 更新字符串
if j - i + 1 < gap:
gap = j - i + 1
res = s[i:i + gap]
i += 1 #更新区间
return res
螺旋矩阵大模拟
方阵
总体思路:确定循环的圈数 维护每一圈的开始坐标 以左闭右开作为每次循环的边界条件1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
# 构建模拟矩阵
matrix = [[0 for _ in range(n)] for _ in range(n)]
# 一圈一圈填充 总循环圈数
loops = n // 2
# n为奇数时需要填中心点
mid = n // 2
# 起始点
start_x, start_y, count = 0, 0, 1
# 左闭右开的原则 上右下左依次填充 每次循环宽度减 1
for offset in range(1, loops + 1):
# n-offset 左闭右开
# 上行 从右到左填充
for i in range(start_y, n - offset):
matrix[start_x][i] = count
count += 1
# 右列 从上到下
for i in range(start_x, n - offset):
matrix[i][n - offset] = count
count += 1
# 下行 从右到左
for i in range(n - offset, start_y, -1):
matrix[n - offset][i] = count
count += 1
# 左列 从下到上
for i in range(n - offset, start_x, -1):
matrix[i][start_y] = count
count += 1
start_x += 1
start_y += 1
if n % 2 != 0:
matrix[mid][mid] = count
return matrix
普通矩阵
比较通用的解法,从右上角剥离: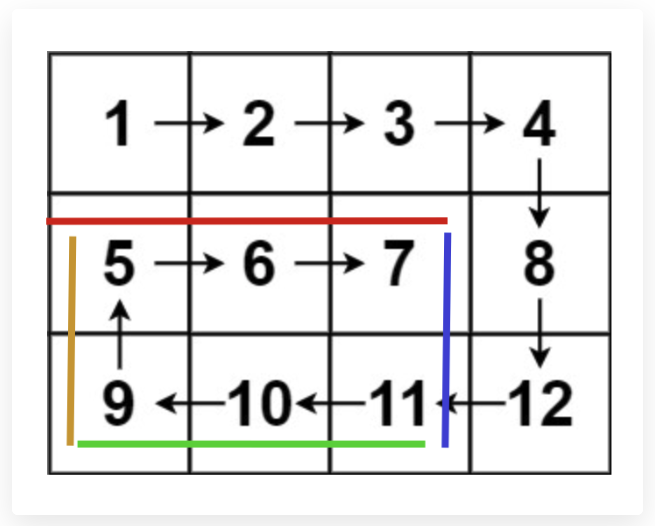
54.螺旋数组1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix or not matrix[0]:
return list()
res = []
m = len(matrix)
n = len(matrix[0])
max_len = m * n
# 维护边界 上下左右
left, right = 0, n - 1
top, bottom = 0, m - 1
# 从上到下 从右到左剥离矩阵
# 左闭右闭 所以要+1 -1控制边界 while len(res) < max_len:
# 上行 从左到右
if top <= bottom:
for i in range(left, right + 1):
res.append(matrix[top][i])
top += 1
# 右列 从上到下
if left <= right:
for i in range(top, bottom + 1):
res.append(matrix[i][right])
right -= 1
# 下行 从右向左
if top <= bottom:
for i in range(right, left - 1, -1):
res.append(matrix[bottom][i])
bottom -= 1
# 左列 从下向上
if left <= right:
for i in range(bottom, top - 1, -1):
res.append(matrix[i][left])
left += 1
return res
链表
1 | class ListNode: |
虚拟头结点
- 可以处理删除真实头节点的场景,这样不用特判断,最终返回 dummy_head->next 即可。终止条件
1
2
3dummy_head = ListNode(next=head)
return dummyNode.next;1
2
3while cur!=None
while cur.next!=None
203. 移除链表元素1
2
3
4
5
6
7
8
9
10
11class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
# 虚拟头节点
dummy_head = ListNode(next=head)
cur = dummy_head
while cur.next != None:
if cur.next.val == val:
cur.next = cur.next.next
else:
cur = cur.next
return dummy_head.next
递归写法,最后处理头节点1
2
3
4
5
6def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
if head==None:
return None
head.next = self.removeElements(head.next,val)
return head.next if head.val==val else head
链表的增删改查
除了查找操作,都需要从虚拟头节点开始1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69class MyLinkedList:
def __init__(self):
self.size = 0
# 虚拟头节点
self.dummy_head = Node(0)
def get(self, index: int) -> int:
# 下标从0开始 所以应该加上等号
if index < 0 or index >= self.size:
return -1
cur = self.dummy_head.next
while index:
cur = cur.next
index -= 1
return cur.val
def addAtHead(self, val: int) -> None:
node = Node(val)
node.next = self.dummy_head.next
self.dummy_head.next = node
self.size += 1
def addAtTail(self, val: int) -> None:
# 从虚拟头节点开始
node = Node(val)
pre = self.dummy_head
while pre.next:
pre = pre.next
pre.next = node
self.size += 1
def addAtIndex(self, index: int, val: int) -> None:
if index == self.size:
self.addAtTail(val)
return
if index < 0:
self.addAtHead(val)
return
if index > self.size:
return
# 插入到index前
pre = self.dummy_head
while index:
pre = pre.next
index -= 1
node = Node(val)
node.next = pre.next
pre.next = node
self.size += 1
def deleteAtIndex(self, index: int) -> None:
if index < 0 or index >= self.size:
return
pre = self.dummy_head
while index:
pre = pre.next
index -= 1
pre.next = pre.next.next
self.size -= 1
# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)
反转链表
使用双指针的写法,pre维护下一步需要反向链接的节点,cur维护当前节点,并控制向后移动,由于cur反向链接的时候会丢失原来的链接关系,因此需要备份到tmp1
2
3
4
5
6
7
8
9
10
11
12def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
# 双指针
pre, tmp = None, None
cur = head
while cur:
# cur指针向后移动
# cur指针反向指向pre
tmp = cur.next # 备份当前位置指向的下一个节点 便于向后移动
cur.next = pre # 反向链接
pre = cur # 更新当前位置
cur = tmp # 向后移动
return pre
两两交换链表中的节点
24. 两两交换链表中的节点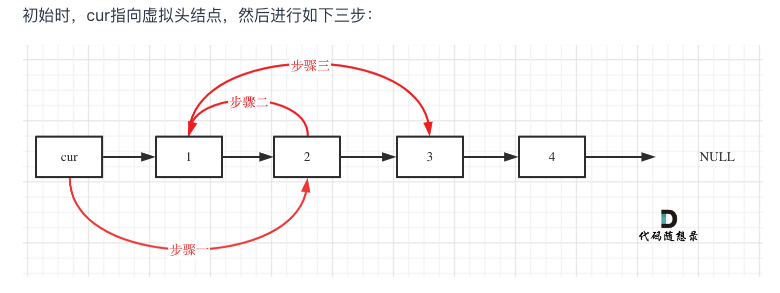
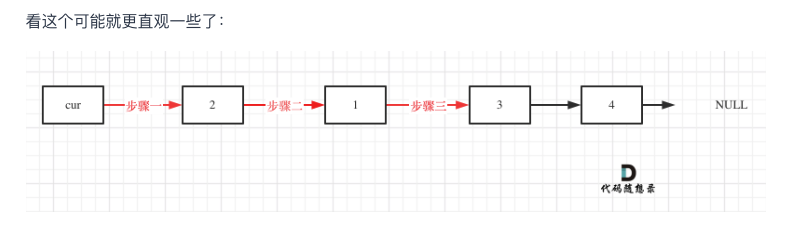
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
dymm_head = ListNode()
dymm_head.next = head
# 能够两两交换需要满足 下一个节点和下下一个节点不为空
cur = dymm_head
while cur.next != None and cur.next.next != None:
# 备份两阶段指向关系
temp1 = cur.next
temp2 = cur.next.next.next
# 链接交换关系
# 左边是目标链接关系 右边往上填空即可
cur.next = cur.next.next
cur.next.next = temp1
cur.next.next.next = temp2
# 移动两位 准备下一轮交换 需使用更新后的cur
cur = cur.next.next
return dymm_head.next
快慢指针
终止条件:fast.next != None
相当于快指针和慢指针的间隔始终为n+11
2
3
4
5
6
7
8
9
10
11
12
13
14def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
# 使用快慢指针
# fast先移动n+1步 再与slow同时移动 当fast到达终点时 slow指向倒数n+1个节点 执行删除操作 dymm_head = ListNode()
dymm_head.next = head
fast, slow = dymm_head, dymm_head
while n and fast.next != None:
fast = fast.next
n -= 1
# fast再多移动一步 方便slow定位到倒数n+1节点
while fast.next != None:
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return dymm_head.next
寻找环的入口
仍然是快慢指针的思想
142. 环形链表 II1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
# 快慢指针
# 快指针每次移动2 慢指针每次移动1
# 第一次相交之后 慢指针停留 新指针从头开始 速度为1
# 二次相遇时即为入口
fast, slow = head, head
# 因为要走两步 所以要判断next.next
while fast != None and fast.next != None:
fast = fast.next.next
slow = slow.next
# 第一次相遇
if fast == slow:
p = head
q = slow
while p != q:
# 第二次相遇
p = p.next
q = q.next
return p
return None
KMP算法
KMP的经典思想就是:当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
时间复杂度:其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
前缀:是指不包含最后一个字符的所有以第一个字符开头的连续子串
后缀:是指不包含第一个字符的所有以最后一个字符结尾的连续子串
前后缀的顺序都是正序,比如aabaa ,长度为4的 前缀有aaba 后缀有abaa
前缀表的作用
- next数组就是一个前缀表
- 前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
- 长度为前1个字符的子串
a,最长相同前后缀的长度为0。(注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。) - 前缀表的作用
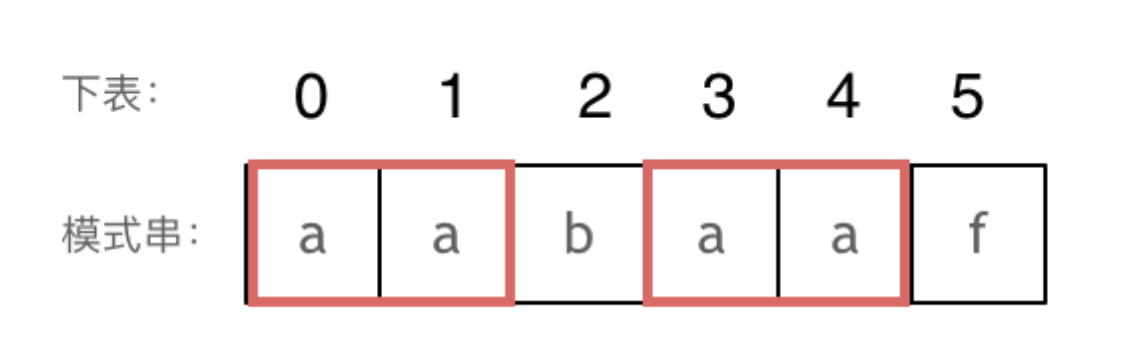
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面(f),那么我们找到与其相同的前缀的后面(b)重新匹配就可以了。
简单来说,即便aa后面的f匹配失败,但是f之前的aa是匹配成功的,而f之前的aa又与b前面的aa相同,即为最长相等子串,前缀表中记录的正是这一信息,下次匹配直接从相同的前缀下一位匹配就好,因为b之前的前缀aa一定是可以匹配上的,不然f之前的aa也不会匹配,更不会到f这边才发生匹配失败的错误。
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
生成前缀表/next数组
针对模式串的操作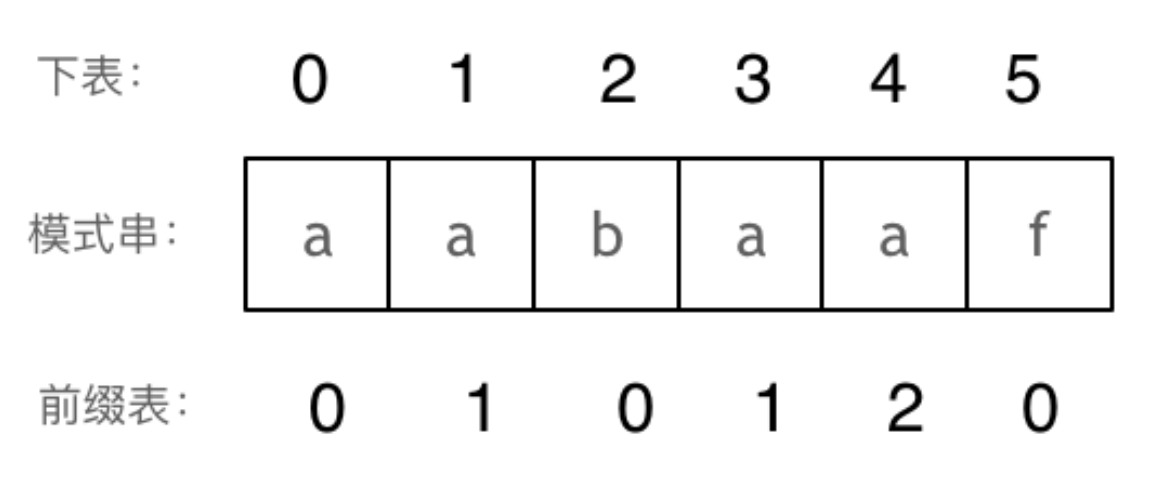
模式串与前缀表对应位置的数字表示的就是:下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
例如:i=4,对应字符串aabaa,对大相等的前后缀分别是aa,aa,为2.
- 代码:
构造next数组其实就是计算模式串s,前缀表的过程。 主要有如下三步:
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
next数组不减1的写法,这样可以保证next数组存的就是会退后前缀的下一个位置,可以直接开始新一轮匹配1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def getnext(self, s):
# 模式串
len_s = len(s)
next = ['' for i in range(len_s)] # 与模式串长度相同
j = 0 # 控制模式穿next数组更新
next[0] = 0
for i in range(1, len_s):
# i从1开始查找
while j > 0 and s[i] != s[j]:
# j要保证大于0,因为下面有取j-1作为数组下标的操作
j = next[j - 1] # 注意这里,是要找前一位 对应的回退位置了
if s[i] == s[j]:
j += 1 # 匹配成功进行下一位匹配
next[i] = j #更新最长前缀长度 注意是for循环中i得下标
return next
前缀表的用法/使用next数组来做匹配
当找到的不匹配的位置, 那么此时要看当前字符的前一个字符的前缀表的数值是多少。
为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。找到最长相同的前缀后再从下一位开始匹配。
next数组既可以就是前缀表,也可以是前缀表统一减一,没特殊的作用,但会导致代码写法不同。
KMP代码
next数组不减1的写法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def strStr(self, haystack: str, needle: str) -> int:
a = len(needle) # 模式串
b = len(haystack) # 文本串
if a == 0:
return 0
next = self.getnext(needle)
j = 0 # 控制模式串
# 外层循环遍历文本串 O(n)
for i in range(b):
while j > 0 and needle[j] != haystack[i]:
j = next[j - 1] # 未匹配成功 回退到上一个位置存储的前缀下标
if needle[j] == haystack[i]:
j += 1 # 匹配成功后移
if j == a:
# 匹配到末尾 完全匹配上了
return i - a + 1 #返回匹配开始的下标
return -1
找到最小重复子串
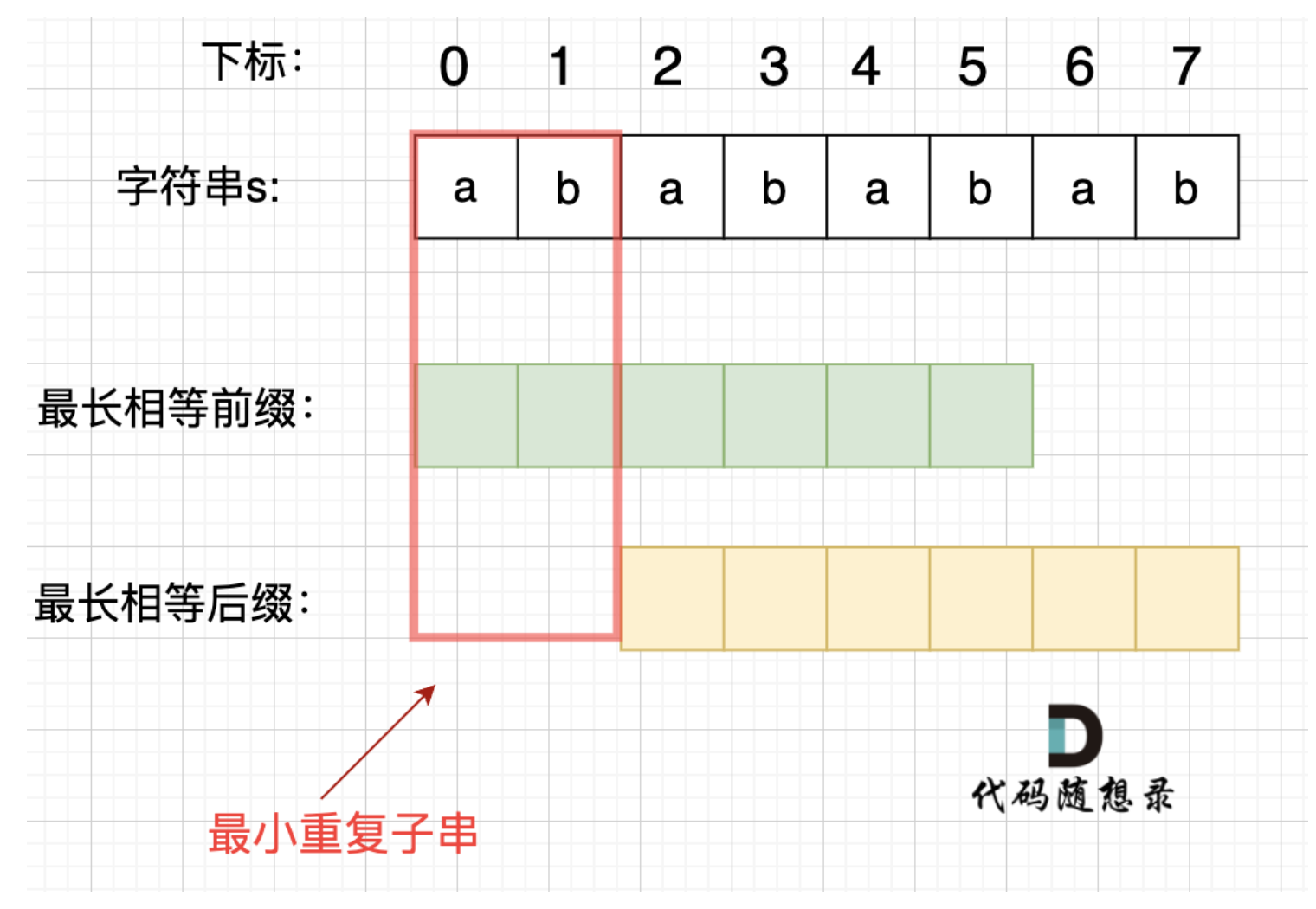
- 最长相等前后缀的规则,当一个字符串由重复子串组成的,最长相等前后缀不包含的子串就是最小重复子串。
- 如果
len % (len - next[-1]) == 0,则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ,说明该字符串有重复的子字符串。解释:
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度,也就是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。
这个周期对应的就是最小重复子串:
长度len - next[-1],区间[0:len - next[-1]]
最长相等前后缀长度:存储在next数组最后一位,next[-1]
- next数组最后一位不是0就是最长相等前后缀长度。(0的话其实就代表没有公共子串)
栈和队列
栈:先进后出
队列:先进先出
- 使用栈模拟队列
关键思想:使用两个栈分别维护新增和删除元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class MyQueue:
# 使用list模拟栈
# 使用栈模拟队列
def __init__(self):
self.stack_in = [] # 进栈
self.stack_out = [] # 出栈
def push(self, x: int) -> None:
# 加到队列结尾
self.stack_in.append(x)
def pop(self) -> int:
# 弹出队首的元素
# 由于队列是先进先出 所以队首为最早加入的元素 if self.empty():
return None
if self.stack_out:
return self.stack_out.pop()
else:
# 将入栈的的元素反向添加到出栈 用栈得先进后出 模拟队列的先进先出
self.stack_out.extend(self.stack_in[::-1])
self.stack_in = []
return self.stack_out.pop()
def peek(self) -> int:
# 查看对首的元素 并不弹出 可以看到 与pop相比 少了弹出的操作
this_pop = self.pop()
if this_pop:
self.stack_out.append(this_pop)
return this_pop
else:
return None
def empty(self) -> bool:
return not self.stack_in and not self.stack_out
使用队列模拟栈
关键思想:使用队列的循环插入弹出,模拟栈的先进先出1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class MyStack:
# 使用deque实现stack
# 先进先出 -> 先进后出
def __init__(self):
self.que = deque()
def push(self, x: int) -> None:
self.que.append(x)
def pop(self) -> int:
# 弹出最晚添加的
# 将队列原有的n-1个元素去除 放到最后一个元素后面 弹出原先的最后一个元素即可
if self.empty():
return None
for i in range(len(self.que) - 1):
self.que.append(self.que.popleft())
return self.que.popleft()
def top(self) -> int:
# 查看栈顶的元素 即最新加入的元素
return self.que[-1]
def empty(self) -> bool:
return not self.que
单调队列
使用deque实现单调队列
- 队列出口维护最大或者最小值
- 每次入队都要保证单调性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class MyQueue: # 单调队列(从大到小
def __init__(self):
self.queue = deque() # 这里需要使用deque实现单调队列,直接使用list会超时
# 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。(为什么要判断值与队头相等,我理解的是,窗口要向后滑一位,因此要确保上一个窗口的开头元素要被弹出,因为只有他不会属于移动后的窗口)
# 同时pop之前判断队列当前是否为空。
def pop(self, value):
if self.queue and value == self.queue[0]:
self.queue.popleft() # list.pop()时间复杂度为O(n),这里需要使用collections.deque()
# 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
# 这样就保持了队列里的数值是单调从大到小的了。
def push(self, value):
while self.queue and value > self.queue[-1]:
self.queue.pop() # 弹右侧 保证当前队列单调递减
self.queue.append(value)
# 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
def front(self):
return self.queue[0]
239.滑动窗口最大值
单调队列实现1
2
3
4
5
6
7
8
9
10
11
12class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
result = []
for i in range(k): # 先将前k的元素放进队列 第一个窗口
que.push(nums[i])
result.append(que.front()) # result 记录前k的元素的最大值
for i in range(k, len(nums)): # i维护窗口结束下标
que.pop(nums[i - k]) # 滑动窗口移除最前面元素(上一个窗口开头的元素)
que.push(nums[i]) # 滑动窗口前加入最后面的元素(当前窗口最新加入的元素)
result.append(que.front()) # 记录对应的最大值
return result
单调栈
单调栈一般都会有特点,一个连续序列,对于每个序列都要找左边或右边最大或最小。说白了,如果你读题后有这样的感觉,一字长龙队,问队里每个人你最远能看到都有谁的头比你高或比你低,那9成是单调栈,而且是最高是递减栈,最低是递增栈。
优先队列 (披着队列外衣的堆)
堆
堆是一棵完全二叉树,树中每个结点的值都不小于(或不大于)其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆,小于等于左右孩子就是小顶堆。
- 优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
- 优先级队列对外接口只是从队头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列。
- 优先级队列内部元素是自动依照元素的权值排列。
场景:
- 要统计元素出现频率(可以使用map来进行统计)
- 对频率排序(对频率进行排序,可以使用一种 容器适配器优先级队列。)
- 找出前K个高频元素
a. 不用对整个数组进行排序, 只需要维护k个有序的序列就可以了,所以使用优先级队列是最优的。
b. 要用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。
c. 找出前K个高频元素,因为小顶堆先弹出的是最小的,所以倒序来输出到数组
1 | class Solution: |
堆
但凡遇到在动态过程中取最值的要求,肯定要使用有序数据结构,我们常用的数据结构就是二叉堆和平衡二叉搜索树了。
图
广度优先搜索 BFS
使用广度优先搜索可以计算出无向图中根结点到任意节点的 。
1 | //创建无向图 |
- 遍历二叉树
1 | bool findTarget(TreeNode *root, int k) { |
深度优先搜索 DFS
- 遍历二叉树
1 | bool findTarget(TreeNode* root, int k) { |
两点连通性问题
两点连通性问题为经典问题,一般我们可以使用广度优先搜索或深度优先搜索,以及并查集来解决。
- BFS 相对于DFS更好理解一点,顺着思路就可以写代码
关键思路:
- 构建邻接表
- 层序遍历的同时控制访问状态(更新队列的时候,更新访问状态)
1 | class Solution: |
图的DFS遍历
例如岛屿数量问题
- 岛屿数量
1 | class Solution { |
- 对于边界情况的处理
可以用
direc[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}去遍历四个方向
1 | int direc[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; |
二叉树
定义:1
2
3
4
5class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
满二叉树
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。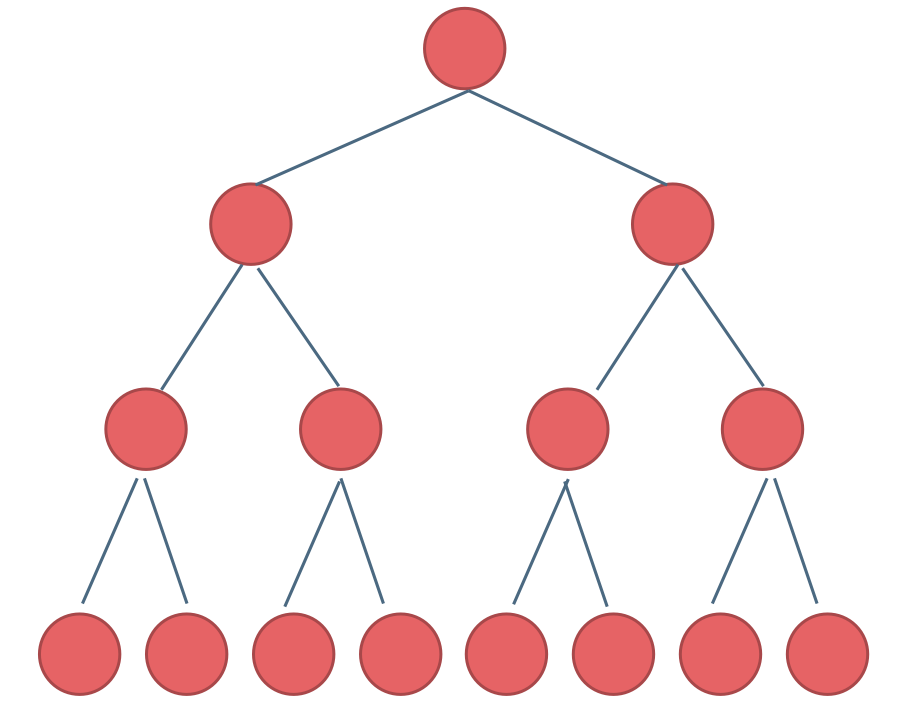
完全二叉树
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。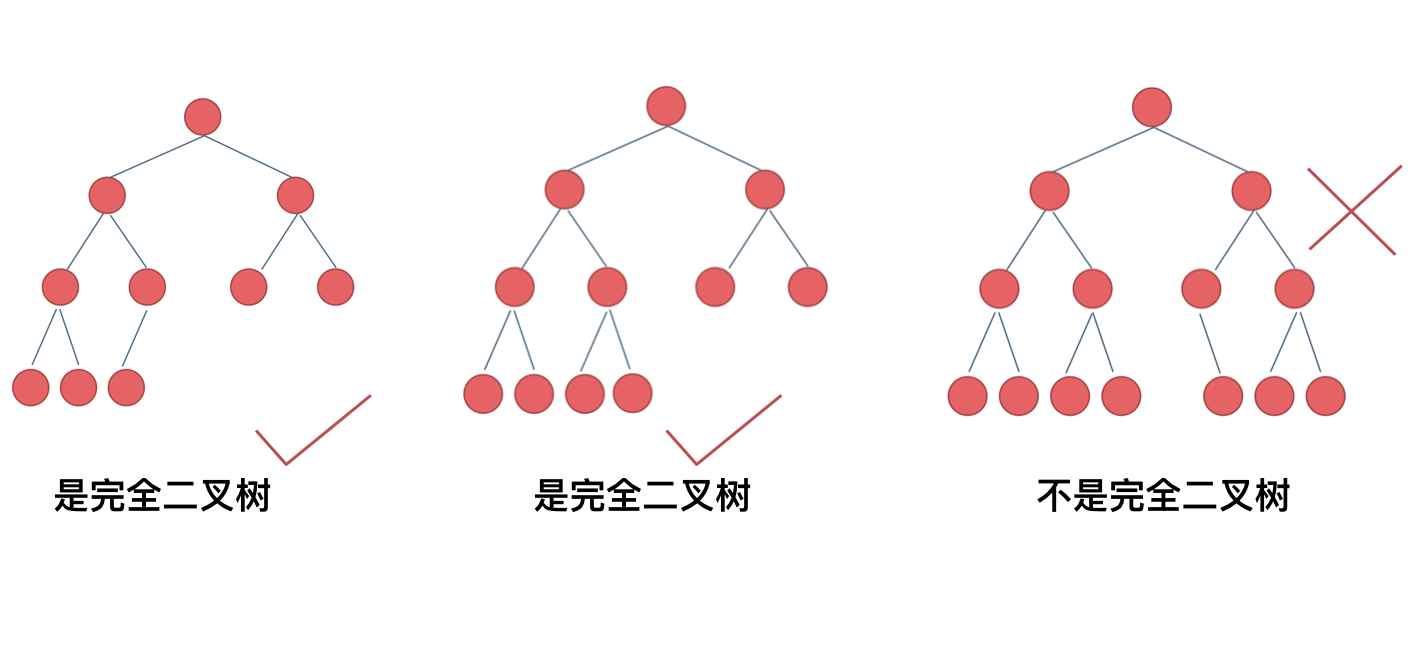
- 优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树,满足左小右大。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
中序遍历下,输出的二叉搜索树节点的数值是有序序列。[3,6,9,10,14,16,19]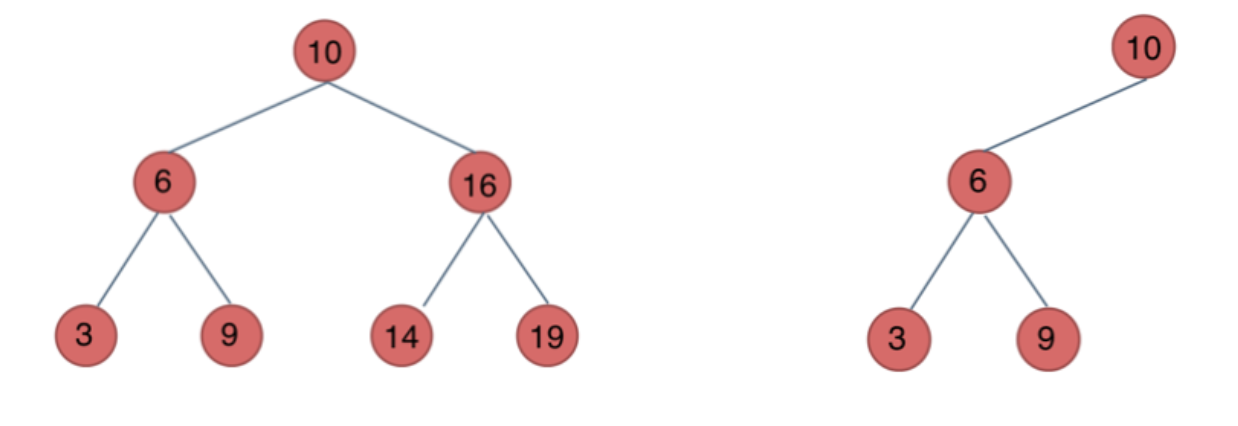
700. 二叉搜索树中的搜索1
2
3
4
5
6
7
8
9
10
11class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
# 左小右大
if not root:
return None
if root.val == val:
return root
elif root.val < val:
return self.searchBST(root.right,val)
else:
return self.searchBST(root.left,val)
记录pre节点处理BST
- 根绝BST左小右大的性质,可以记录pre节点完成一些逻辑
501. 二叉搜索树中的众数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution:
def findMode(self, root: Optional[TreeNode]) -> List[int]:
def inorder(root):
nonlocal res, pre, cnt, max_cnt
if not root:
return
inorder(root.left)
# 处理根节点
if pre is None:
cnt = 1
elif pre.val == root.val:
cnt += 1
else:
cnt = 1
if cnt > max_cnt:
max_cnt = cnt
res.clear()
res.append(root.val)
elif cnt == max_cnt:
res.append(root.val)
pre = root # 更新pre节点
inorder(root.right)
res = []
cnt = 1 # 计数
max_cnt = -inf
pre = None # 记录前一个节点
inorder(root)
return res
二叉搜索树中的插入操作
- 递归到空节点插入
- 只需要在叶子上添加就可以的,不涉及到结构的调整
701.二叉搜索树中的插入操作1
2
3
4
5
6
7
8
9class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return TreeNode(val)
elif root.val > val:
root.left = self.insertIntoBST(root.left,val)
elif root.val < val:
root.right = self.insertIntoBST(root.right,val)
return root
删除二叉搜索树中的节点
分5种情况讨论:
- 未找到待删除节点,返回None
- 左右节点都为空,直接删除返回None
- 当前节点的左子树为空,返回当前的右子树
- 当前节点的右子树为空,返回当前的左子树
- 当前节点左右子树都非空,找到大于左子树的第一个最小的节点,即右子树中最左边的节点node,将当前节点的左子树挂在node的左孩子上,再用当前节点的右子树替换掉当前节点,返回当前的右子树,完成当前节点的删除
450.删除二叉搜索树中的节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root :
return None # 节点为空,返回
if root.val < key :
root.right = self.deleteNode(root.right, key)
elif root.val > key :
root.left = self.deleteNode(root.left, key)
else: # 找到待删除节点
# 当前节点的左子树为空,返回当前的右子树
if not root.left :
return root.right
# 当前节点的右子树为空,返回当前的左子树
if not root.right:
return root.left
# 左右子树都不为空,找到右孩子的最左节点 记为node
# 大于左子树的第一个最小的节点 即右子树中最左边的节点
node = root.right
while node.left :
node = node.left
# 将当前节点的左子树挂在p的左孩子上
node.left = root.left
# 当前节点的右子树替换掉当前节点,完成当前节点的删除
root = root.right
return root
修剪二叉树
BST的节点是左小右大的,因此不能单独的删除某个节点,其子树(左小右大)上并非都能够满足条件,因此应该递归的寻找到合适的节点返回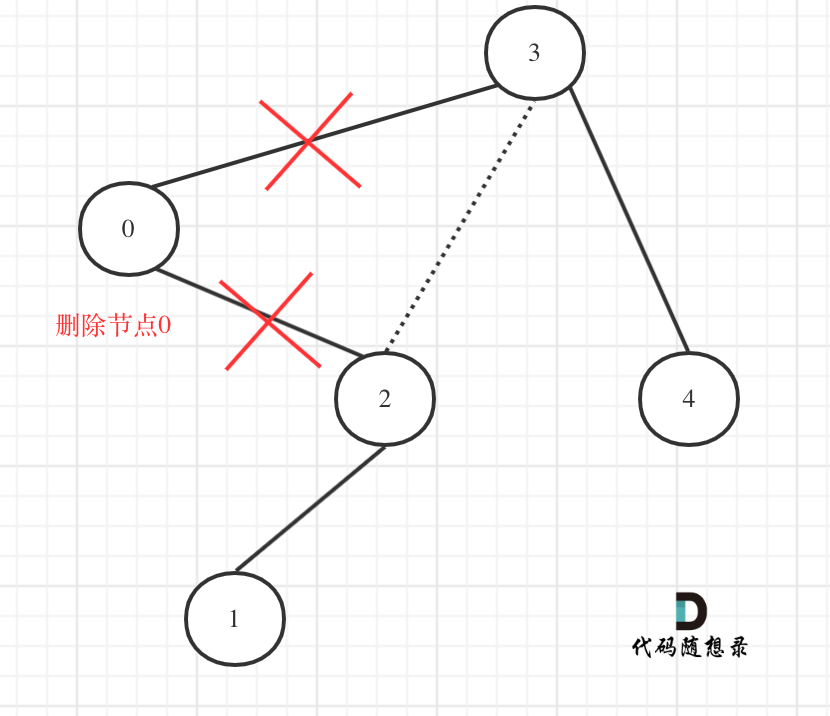
669. 修剪二叉搜索树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution:
def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
if not root:
return None
if root.val < low:
# 左子树肯定更小 将右子树修剪后挂到当前位置
right = self.trimBST(root.right,low,high)
return right
elif root.val > high:
# 将左子树修剪后挂在当前位置
left = self.trimBST(root.left,low,high)
return left
root.left = self.trimBST(root.left,low,high)
root.right = self.trimBST(root.right,low,high)
return root
将有序数组转成BST
- 实际上就是 [[算法笔记-算法&数据结构#构造二叉树]] 的思路
- 确定根节点,切分数组,递归构造左右子树
- 需要注意的是,构造平衡BST,只需要每次取数组中间元素即可
108. 将有序数组转换为二叉搜索树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if len(nums)==0:
return None
# 取根节点索引 数组中间值
root_index = len(nums)//2
root_val = nums[root_index]
root = TreeNode(root_val)
# 分割
nums_left = nums[:root_index]
nums_right = nums[root_index+1:]
# 递归构建左右子树
root.left = self.sortedArrayToBST(nums_left)
root.right = self.sortedArrayToBST(nums_right)
return root
把二叉搜索树转换为累加树
- 中序遍历的反向过程,右中左
- 从图中也可以看到,累加的过程是从右下角开始的
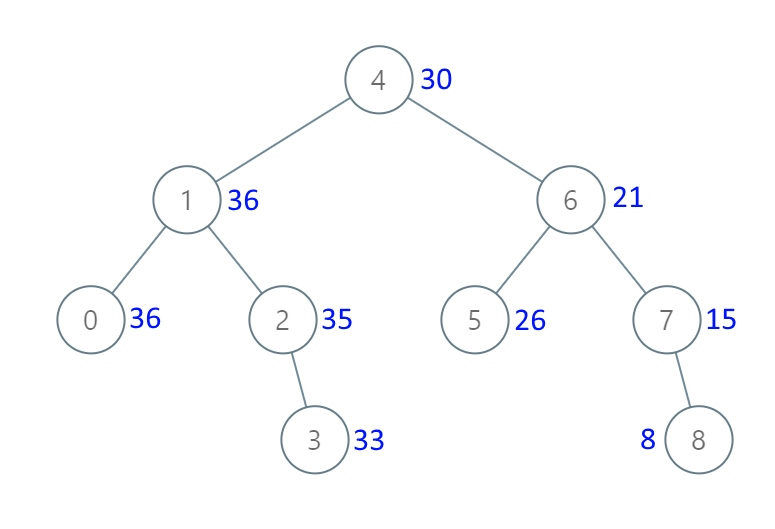
538. 把二叉搜索树转换为累加树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 实际上是有序数组从后向前加和
# 正好是中序遍历的逆向过程def inorder(root):
if not root:
return
nonlocal pre
# 逆向中序遍历 右中左
inorder(root.right)
root.val += pre
pre = root.val
inorder(root.left)
pre = 0 # 记录上一个节点的值
inorder(root)
return root
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:
- 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
二叉树遍历——递归
- 递归加上
@functools.lru_cache可以加速 - 在 Python 的 3.2 +版本中,引入了一个非常优雅的缓存机制,即
functool模块中的lru_cache装饰器,可以直接将函数或类方法的结果缓存住,后续调用则直接返回缓存的结果。 - 但是参数不能有list
递归
- 回溯是递归的副产品,只要有递归就会有回溯。
递归+回溯写法
1
2
3
4
5
6traversal(root->left, depth + 1); // 隐藏着回溯
// 相当于
depth++;
traversal(root->left, depth);
depth--;
递归时要拷贝list的值!!![:]1
res.append(cur_path[:])
搜索一条边的写法
1 | if (递归函数(root->left)) return ; |
搜索整个树写法
1 | left = 递归函数(root->left); // 左 |
区别:
在递归函数有返回值的情况下:如果要搜索一条边,递归函数返回值不为空的时候,立刻返回,如果搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。
如何选择使用哪种遍历方式
- 首先应该明确节点的处理顺序,是需要自上而下(前序遍历),还是自底向上(后序遍历),还是从左向右(中序)
- 甚至可以使用反中序(自右向左)[[算法笔记-算法&数据结构#把二叉搜索树转换为累加树]]
- 尤其在二叉搜索树(BST)中,中序遍历用的较多,因为左中右的遍历顺序,正好是一个有序数组
前序遍历
- 根左右
1
2
3
4
5
6def preorder(self, root, res):
if not root:
return
res.append(root.val) # 根
self.preorder(root.left, res) # 左
self.preorder(root.right, res) # 右
中序遍历
中序遍历下,输出的二叉搜索树节点的数值是有序序列。
- 左根右
1
2
3
4
5
6
7def inorder(self, root, res):
if not root:
return
# 左根右
self.inorder(root.left, res)
res.append(root.val)
self.inorder(root.right, res)
后序遍历
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
- 左右根
1
2
3
4
5
6
7def postorder(self, root, res):
if not root:
return
# 左右根
self.postorder(root.left, res)
self.postorder(root.right, res)
res.append(root.val)
二叉树的遍历——迭代
- 层序遍历,用栈模拟遍历过程,添加空指针标记上一个元素是待处理的节点。
- 迭代法的由于使用栈实现,左右节点添加顺序应改反过来
- 每添加完根节点后添加空节点做标记
st.push(node);st.push(NULL); - 因此,只有遇到空节点的时候,才将下一个节点放进结果集
前序遍历
- 右左根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
中序遍历
- 右根左
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)
st.push(node); // 根
st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.top(); // 重新取出栈中元素
st.pop();
result.push_back(node->val); // 加入到结果集
}
}
return result;
}
};
后序遍历
- 根右左
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 根
st.push(NULL);
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
层序遍历
队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
102.二叉树的层序遍历1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
# 层序遍历
if not root:
return []
que = deque()
que.append(root)
# que =deque([root]) 要加[]
res = list()
while que:
size = len(que) # 要提前计算当前层要遍历几个节点
temp = list()
for _ in range(size):
cur = que.popleft()
temp.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res.append(temp)
return res
翻转二叉树
想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
- 这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次
226. 翻转二叉树1
2
3
4
5
6
7
8
9class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 前序遍历
if not root:
return root
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
左节点之和
404. 左叶子之和1
2
3
4
5
6
7
8
9
10
11
12
13class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
# 一定要满足左叶子节点条件
# 左节点不为空 且 左节点没有左右孩子
if not root:
return 0
# 后序遍历
left_tree_val = self.sumOfLeftLeaves(root.left)
right_tree_val = self.sumOfLeftLeaves(root.right)
cur_node_val = 0
if root.left and not root.left.left and not root.left.right:
cur_node_val = root.left.val
return left_tree_val + right_tree_val + cur_node_val
记录路径
113. 路径总和 II1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
def preorder(root, targetSum, cur_path, cur_sum):
nonlocal res
if not root.left and not root.right:
if cur_sum + root.val == targetSum:
res.append(cur_path[:])
if root.left:
cur_path.append(root.left.val)
preorder(root.left, targetSum, cur_path, cur_sum + root.val)
cur_path.pop()
if root.right:
cur_path.append(root.right.val)
preorder(root.right, targetSum, cur_path, cur_sum + root.val)
cur_path.pop()
if not root:
return []
res = list()
preorder(root, targetSum, [root.val], 0)
return res
构造二叉树
中序+后序
- 以 后序数组 的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。
- 一层一层切下去,每次后序数组最后一个元素就是根节点元素。
- 有一个很重要的点,就是中序数组大小一定是和后序数组的大小相同的,左右子树当然也是(这是必然)。
- 因此,中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
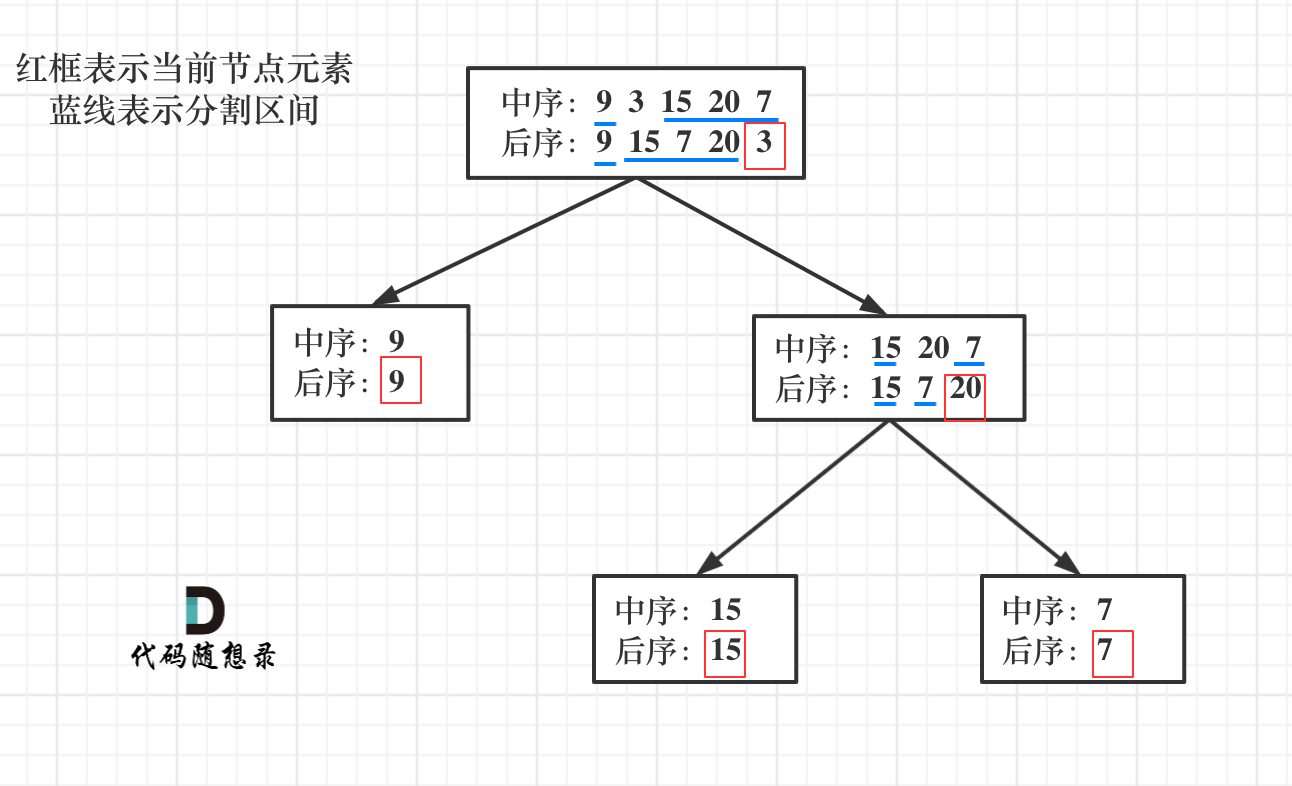
106.从中序与后序遍历序列构造二叉树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. (递归终止条件)
if not postorder:
return None
# 第二步: 后序遍历的最后一个就是当前的中间节点.
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
postorder_left = postorder[:len(inorder_left)]
postorder_right = postorder[len(inorder_left): len(postorder) - 1]
# 第六步: 递归 构建左右子树
root.left = self.buildTree(inorder_left, postorder_left)
root.right = self.buildTree(inorder_right, postorder_right)
return root
前序+中序
- 根据前序数组找到根节点,切割中序数组
- 按切割后的左右中序数组大小对应切割,除当前根节点之外的其他元素
- 递归构建二叉树
105.从前序与中序遍历序列构造二叉树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not preorder:
return None
# 第二步: 前序遍历的第一个就是当前的中间节点.
root_val = preorder[0]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割preorder数组. 得到preorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
preorder_left = preorder[1:1 + len(inorder_left)]
preorder_right = preorder[1 + len(inorder_left):]
# 第六步: 递归
root.left = self.buildTree(preorder_left, inorder_left)
root.right = self.buildTree(preorder_right, inorder_right)
return root
合并二叉树
617. 合并二叉树
递归的方式合并到tree11
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
# 前序遍历
if not root1:
return root2
if not root2:
return root1
# 处理合并新的根节点
root1.val = root1.val+root2.val
# 合并左子树
root1.left = self.mergeTrees(root1.left,root2.left)
# 合并右子树
root1.right = self.mergeTrees(root1.right,root2.right)
return root1
最近公共祖先
- 从下向上找
- 后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
236. 二叉树的最近公共祖先1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if root == p or root == q or root == None:
return root
# 后序遍历 天然的自下而上的回溯过程 处理完左右子树再处理根节点
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
# 处理根节点
if left and right: # 找到了
return root
elif left and not right: # 在左子树
return left
elif not left and right: # 在右子树
return right
else: # 没找到
return None
- 对于二叉搜索树,如果当前节点的值在区间[p,q],那么说明当前节点就是「分岔点」。此时,p 和 q 要么在当前节点的不同的子树中,要么其中一个就是当前节点。
- 因此第一次找到的位于区间[p,q]的节点就是最近公共祖先。
235. 二叉搜索树的最近公共祖先1
2
3
4
5
6
7
8
9
10
11
12
13class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root:
return
# 利用BST的性质
if root.val > p.val and root.val > q.val:
# 太大了 在左边寻找
return self.lowestCommonAncestor(root.left, p, q)
elif root.val < p.val and root.val < q.val:
# 太小了 在右边寻找
return self.lowestCommonAncestor(root.right, p, q)
else:
return root
回溯
- 回溯是递归的副产品,只要有递归就会有回溯
- 回溯法解决的问题都可以抽象为树形结构
- 回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
- 返回值一般void
- 可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。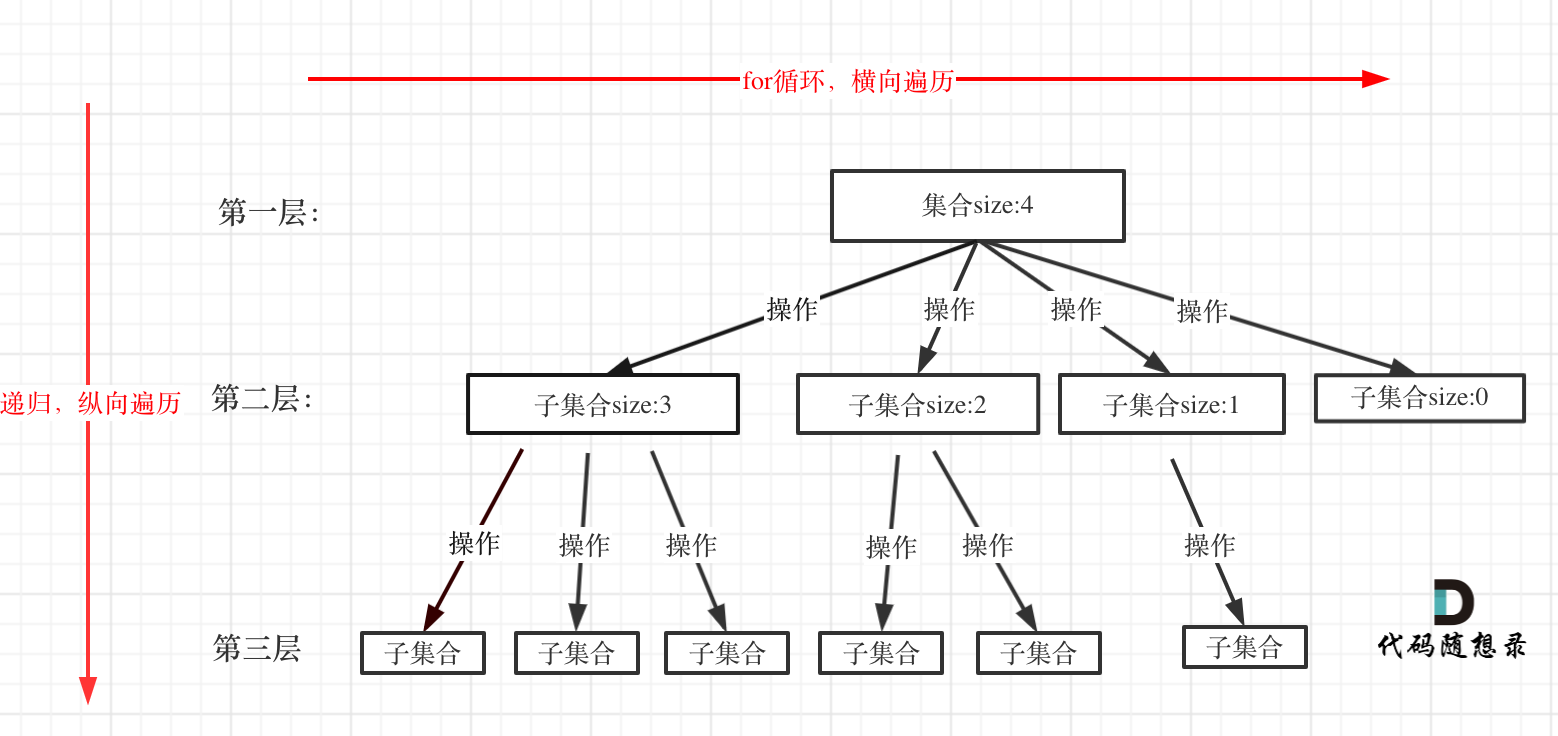
注意图中,特意举例集合大小和孩子的数量是相等的!
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
模板:1
2
3
4
5
6
7
8
9
10
11
12void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
说明:
- 先判断终止条件
- for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
- backtracking这里自己调用自己,实现递归。
剪枝: - 可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
组合问题
组合
图解: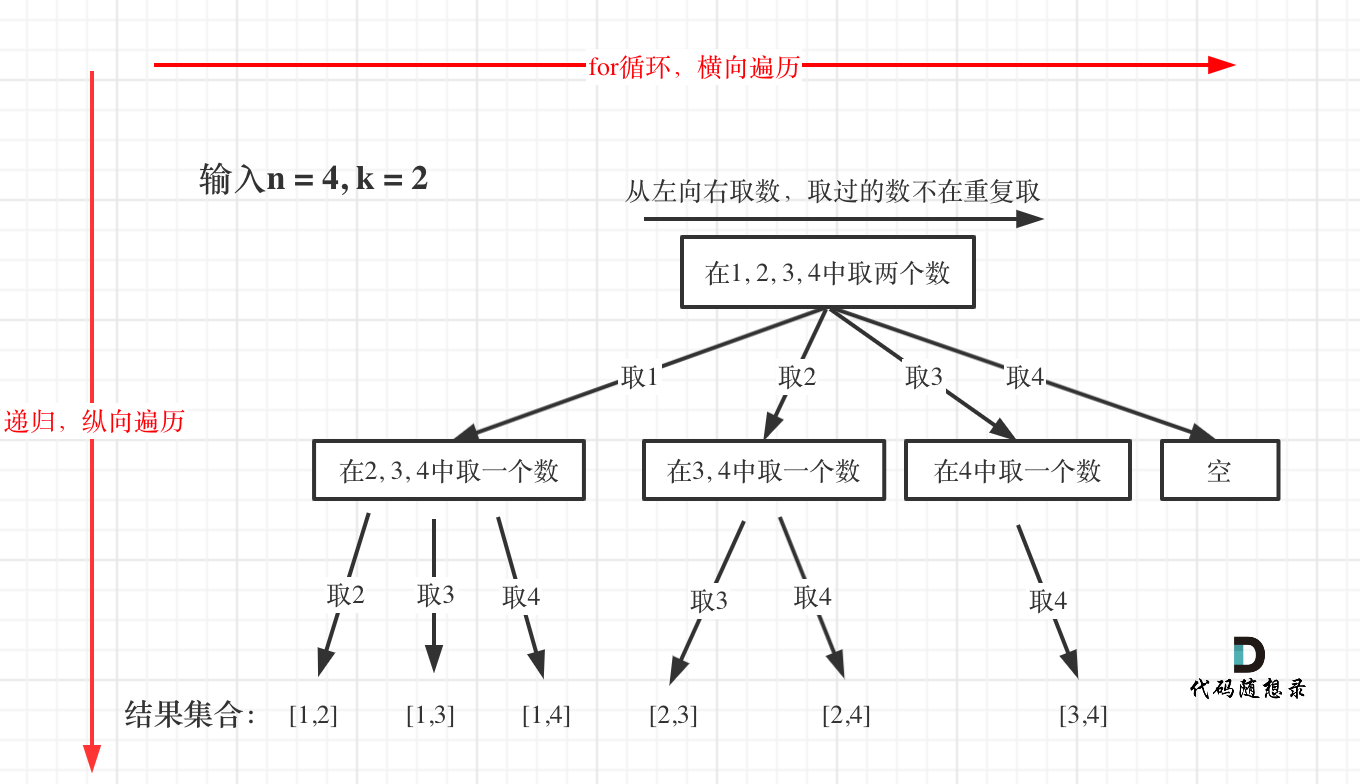
77. 组合start_index比较重要,记录开始计算的位置,避免重复的组合出现
拷贝path要使用[:]
1 | class Solution: |
电话号码的字母组合
- 在for循环外控制当前遍历的集合
- 在for循环内控制递归的层级
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution:
def letterCombinations(self, digits: str) -> List[str]:
def backtracking(digits, start_index):
nonlocal path,res,letterMap
if start_index == len(digits):
res.append(''.join(path))
return
# 当前字符集
cur_digits = letterMap[int(digits[start_index])] # 控制当前集合
for i in cur_digits:
path.append(i) # 当前集合都是同样的层数
backtracking(digits, start_index + 1)
path.pop()
letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz", # 9
]
if digits=="":
return []
path = []
res = []
backtracking(digits, 0)
return res
组合总和-可重复
- 元素可以重复使用,关键点在于,递归时,从当前节点
i单开始,表示当前节点可以被多次使用(下次递归,从当前节点开始,则是重复使用) - 题目要求只是同一个 数字可以 无限制重复被选取,递归的过程仍然是数组缩小的,因此仍需要
start_index避免路径重复
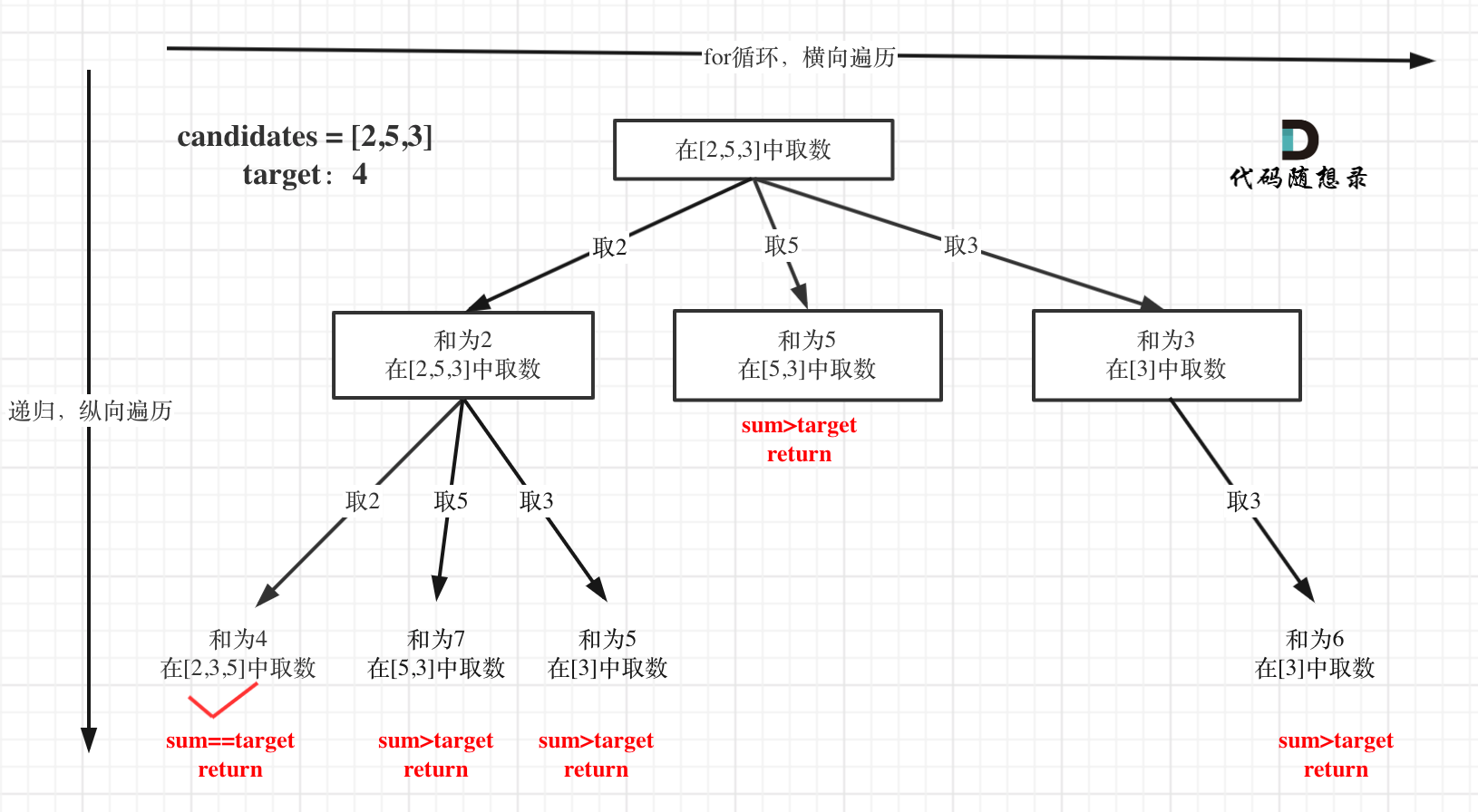
39. 组合总和 ^idxxj51
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtracing(candidates, target, sum_num, start_index):
nonlocal res, path
if sum_num == target:
res.append(path[:])
return
elif sum_num > target:
return
for i in range(start_index, len(candidates)):
path.append(candidates[i])
sum_num += candidates[i]
backtracing(candidates, target, sum_num, i) # 关键点 用i 而不是i+1 表示当前节点可以重复
sum_num -= candidates[i]
path.pop()
res = []
path = []
backtracing(candidates, target, 0, 0)
return res
组合去重
相比于[[算法笔记-算法&数据结构#^idxxj5]]不同之处在于,数组中有重复元素,要避免组合重复应该在遍历的过程中,控制在同一层中,相同的元素只使用一次,而不能简单的对原数组去重,因为向下递归的过程,要合法的用到所有元素。
还可参考使用set()去重:[[算法笔记-算法&数据结构#递增子序列]]
还可以使用used数组去重:[[算法笔记-算法&数据结构#全排列去重]]需要注意的是:使用set去重的版本相对于used数组的版本效率都要低很多
1. 主要是因为程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且insert的时候其底层的符号表也要做相应的扩充,也是费时的。 2. **而使用used数组在时间复杂度上几乎没有额外负担!使用set去重,不仅时间复杂度高了,空间复杂度也高了**
- 关键点在于:先对原数组 排序 将相同的元素放在一起 方便去重
- 循环时控制同一层,不能遍历 相同的的元素。同一层:同一个for循环就是一层
- 每个元素只能使用一次,递归时用
i+1即可1
2if i > start_index and candidates[i] == candidates[i - 1]:
continue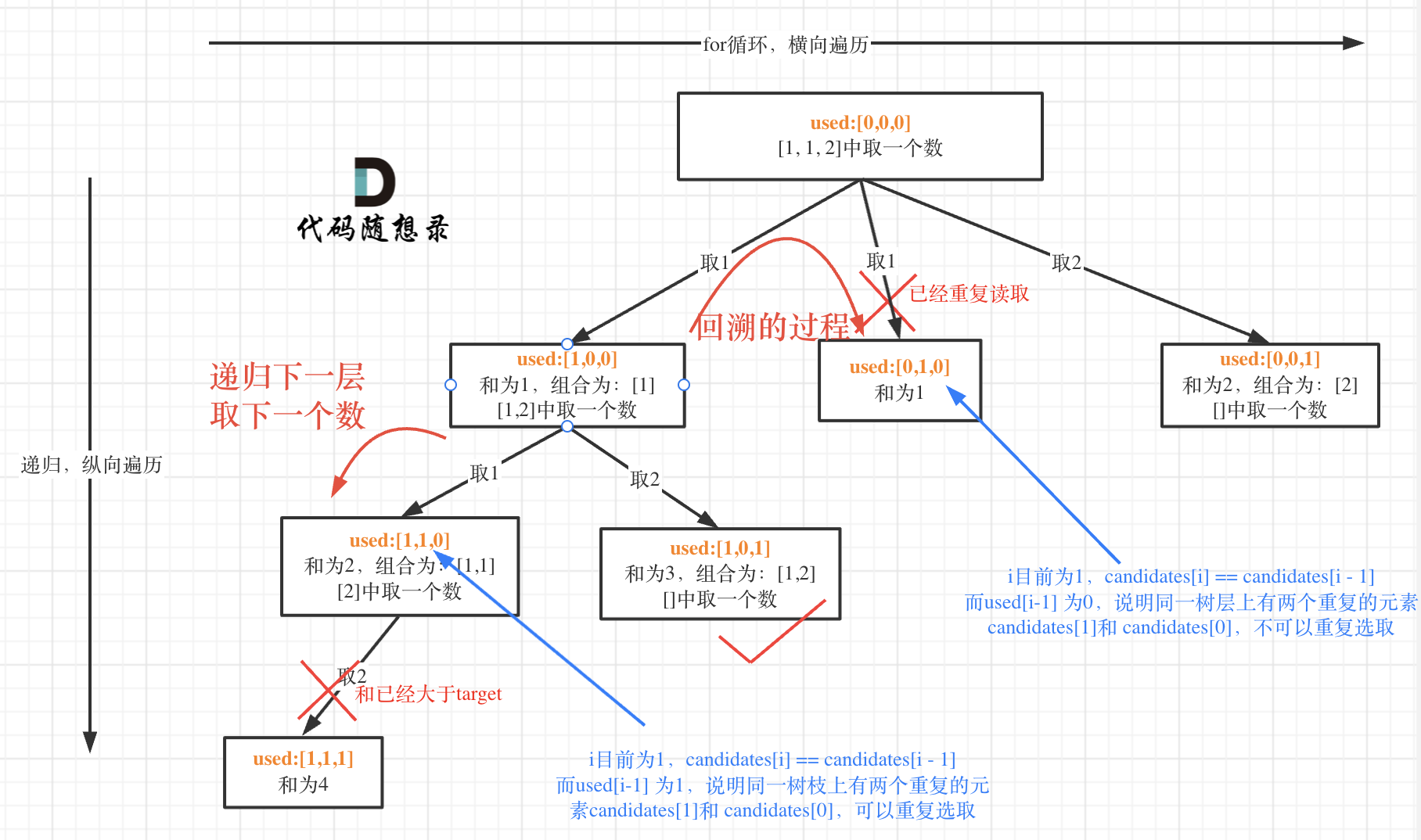
40. 组合总和 II1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
def backtracing(candidates, target, sum_num, start_index):
nonlocal res, path
if sum_num == target:
res.append(path[:])
return
elif sum_num > target:
return
for i in range(start_index, len(candidates)):
# 为避免集合重复 同一层不遍历相同的元素
if i > start_index and candidates[i] == candidates[i - 1]:
continue
path.append(candidates[i])
sum_num += candidates[i]
backtracing(candidates, target, sum_num, i + 1) # 关键点 用i+1 每个节点只能使用一次
path.pop()
sum_num -= candidates[i]
res = []
path = []
candidates.sort() # 排序 将相同的元素放在一起 方便去重
backtracing(candidates, target, 0, 0)
return res
切割问题
切割逻辑:
- 在同一层循环,从当前轮的起始位置依次向后切割
在
for (int i = start_index; i < s.size(); i++)循环中,我们 start_index,那么[start_index, i]就是要截取的子串。 - 递归时带上下一次切分的开始位置
- 终止条件,切割点移到末尾
start_index == len(s)1
2path.append(s[start_index:i + 1])
backtracing(s, i + 1)
分割回文串
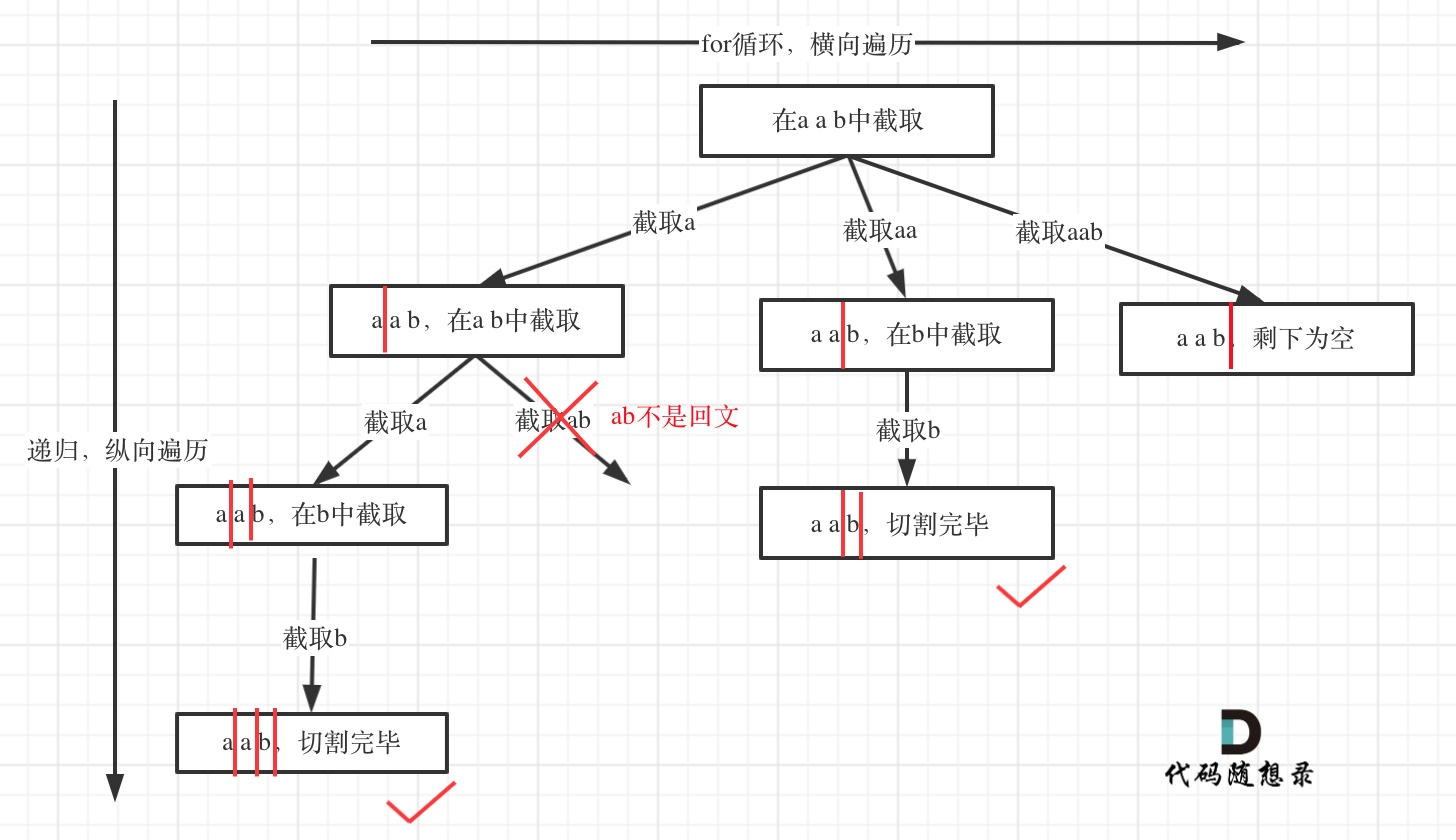
131. 分割回文串1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution:
def partition(self, s: str) -> List[List[str]]:
def backtracing(s, start_index):
nonlocal res, path
if start_index == len(s):
res.append(path[:])
return
# 分割
for i in range(start_index, len(s)):
temp = s[start_index:i + 1]
if temp == temp[::-1]: # 正反序相同就是回文串
path.append(temp)
backtracing(s, i + 1)
path.pop()
else:
continue
if len(s) < 2:
return [[s]]
res = []
path = []
backtracing(s, 0)
return res
还原ip
- 与[[算法笔记-算法&数据结构#切割问题]]不同之处在于,这个道题限制了递归的深度为4,因此在递归的处理逻辑中应该加上。
- 除此之外,分割字符依然是在同一层
for里按位切割 - 递归结束条件除了深度为4,还要满足遍历到字符串结束位置
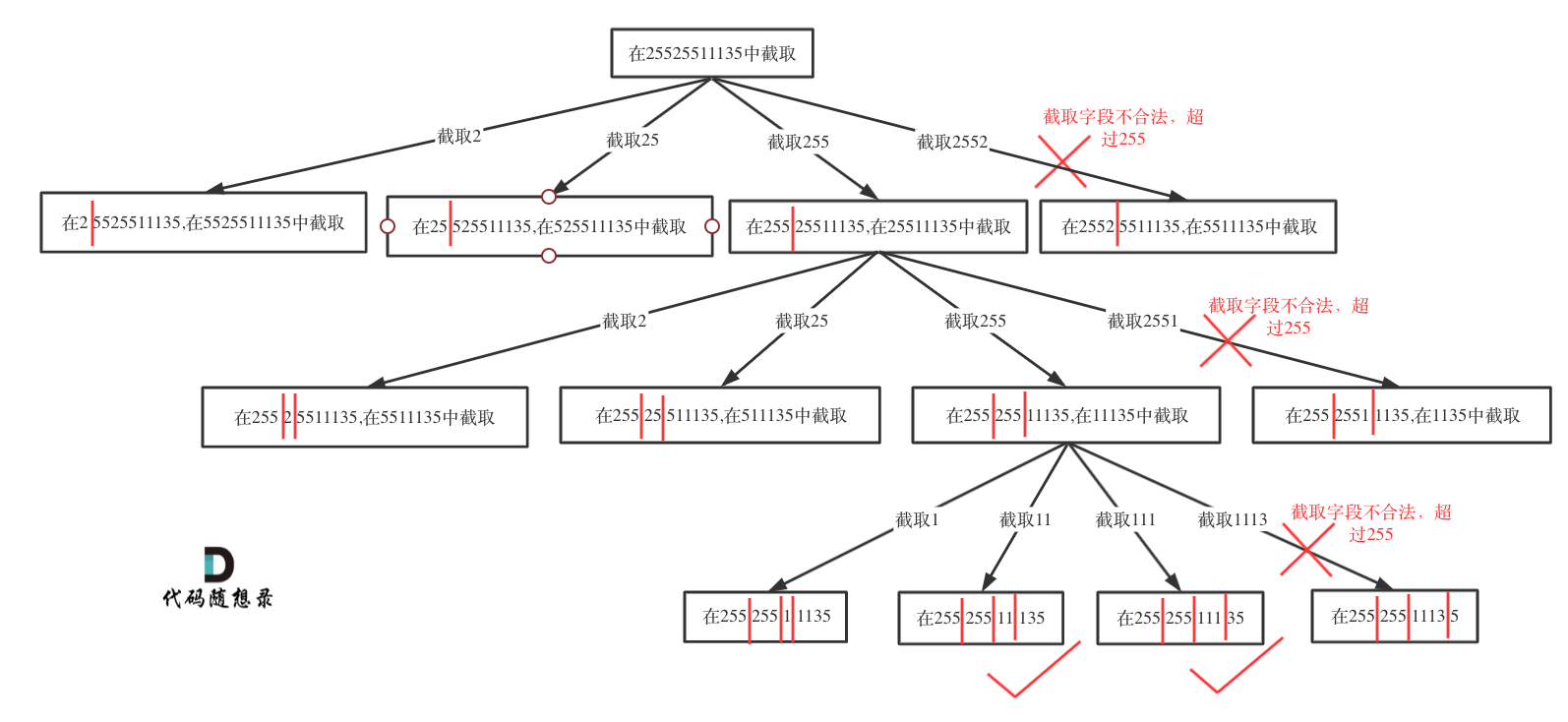
93. 复原 IP 地址1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
# 递归深度四层
def check(s):
# 验证字符串是否合法
if len(s) > 1 and s[0] == '0':
return False
if not s.isdigit():
return False
if 0 <= int(s) <= 255:
return True
return False
def backtracing(s, start_index, depth):
nonlocal res, path
if depth == 4 and start_index == len(s):
cur_path = '.'.join(path[:])
res.append(cur_path)
return
elif depth > 4:
return
# 切割字符串
for i in range(start_index, len(s)):
temp = s[start_index:i + 1]
if check(temp):
path.append(temp)
backtracing(s, i + 1, depth + 1)
path.pop()
else:
break
res = []
path = []
backtracing(s, 0, 0)
return res
子集问题
- 与之前处理组合和切割问题,记录子节点不同,子集问题需要记录所有节点。
查找子集
78.子集1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def backtracing(nums, start_index):
nonlocal res, path
# 记录所有节点
res.append(path[:])
if start_index == len(nums):
return
for i in range(start_index, len(nums)):
path.append(nums[i])
backtracing(nums, i + 1) # 递归到下一层
path.pop()
res = []
path = []
backtracing(nums, 0)
return res
加上去重逻辑:
- 排序后控制,同一层中,相同的元素只递归一次
1
2if i > start_index and nums[i] == nums[i - 1]:
continue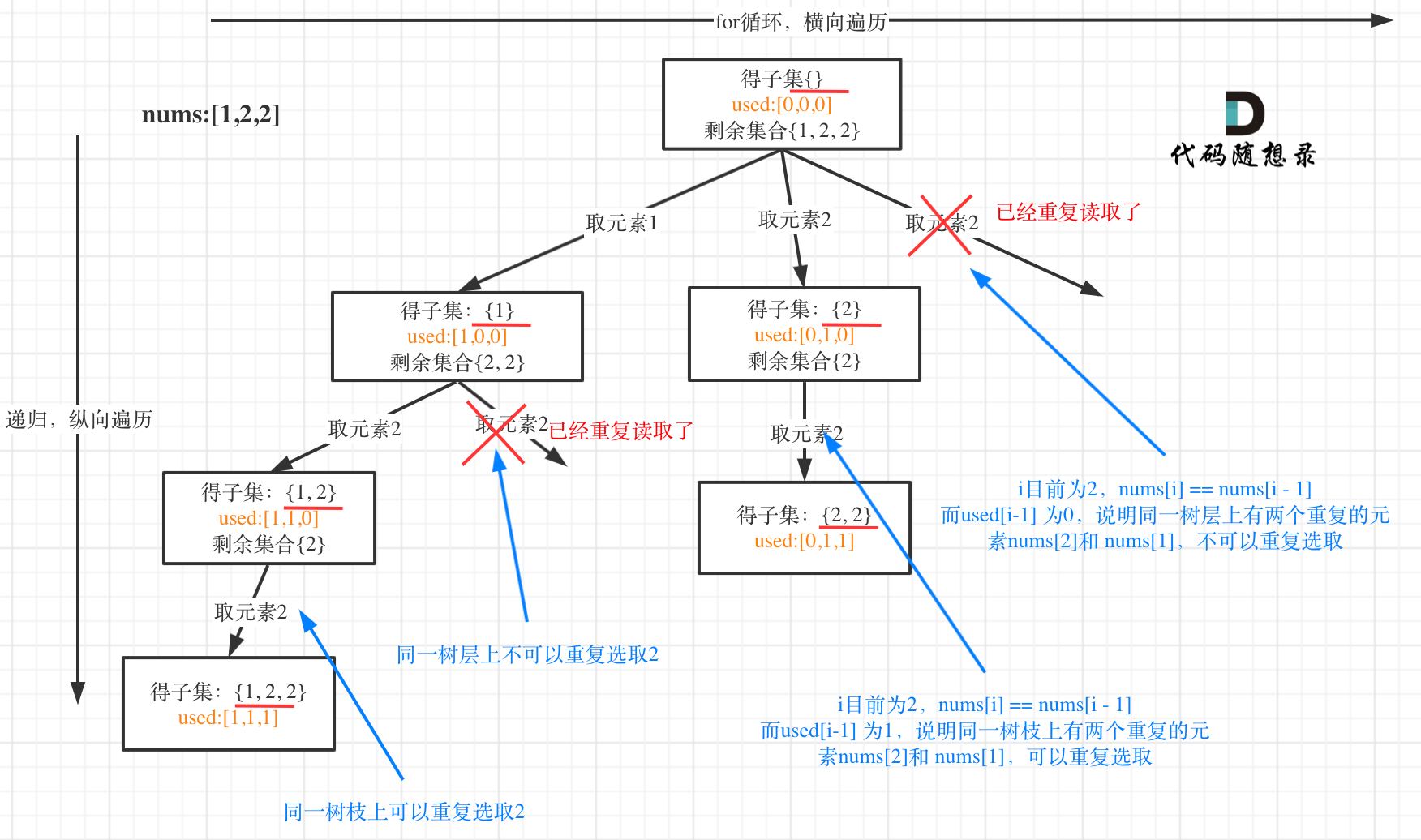
90. 子集 II1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
# 需要排序去重
def backtracing(nums, start_index):
nonlocal res, path
res.append(path[:])
if len(nums) == start_index:
return
for i in range(start_index, len(nums)):
if i > start_index and nums[i] == nums[i - 1]:
continue
else:
path.append(nums[i])
backtracing(nums, i + 1)
path.pop()
res = []
path = []
nums.sort()
backtracing(nums, 0)
return res
递增子序列
- 与[[算法笔记-算法&数据结构#查找子集]]不同之处在于,本题去重时不能对原数组排序,因此在递归时判断当前元素是否与上一次递归的元素相同,变得不可行。
原先的去重方法:1
2if i > start_index and nums[i] == nums[i - 1]:
continue - 考虑到原数组无序,我们的目的是,同层递归时不能递归之前已递归过的元素,否则必然重复。因此使用一个set()记录本层使用过的元素。
1
2if i > start_index and nums[i] in used:
continue - 值得注意的是
used.add(nums[i])结束后不需要手动弹出进行回溯,因为used是一个局部变量,仅在本层生效。
491. 递增子序列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
def backtracing(nums, start_index):
nonlocal res, path
if len(path) > 1:
res.append(path[:])
used = set()
for i in range(start_index, len(nums)):
# 去重 同层不能有重复元素 因为不能对原nums排序,因此要记录本层使用过的节点
if i > start_index and nums[i] in used:
continue
else:
if len(path) == 0:
path.append(nums[i])
used.add(nums[i]) # 不用pop nums[i] 因为set每层都会初始化定义,使用范围仅限本层
backtracing(nums, i + 1)
path.pop()
elif len(path) > 0:
if path[-1] <= nums[i]:
path.append(nums[i])
used.add(nums[i])
backtracing(nums, i + 1)
path.pop()
else:
continue
res = []
path = []
backtracing(nums, 0)
return res
排列问题
- 首先排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
- 排列每次用到的数组都是除自身已使用元素之外的其他元素,因此不必记录切割位置start_index,只需要记录当前分支,哪些元素已经使用过了,因此使用一个全局访问标记数组记录当前路径元素的使用情况。
- 既然是全局访问标记数组,因此要弹出递归前加入的元素,进行回溯
1
2
3used[i] = True
backtracing(nums, used)
used[i] = False
全排列
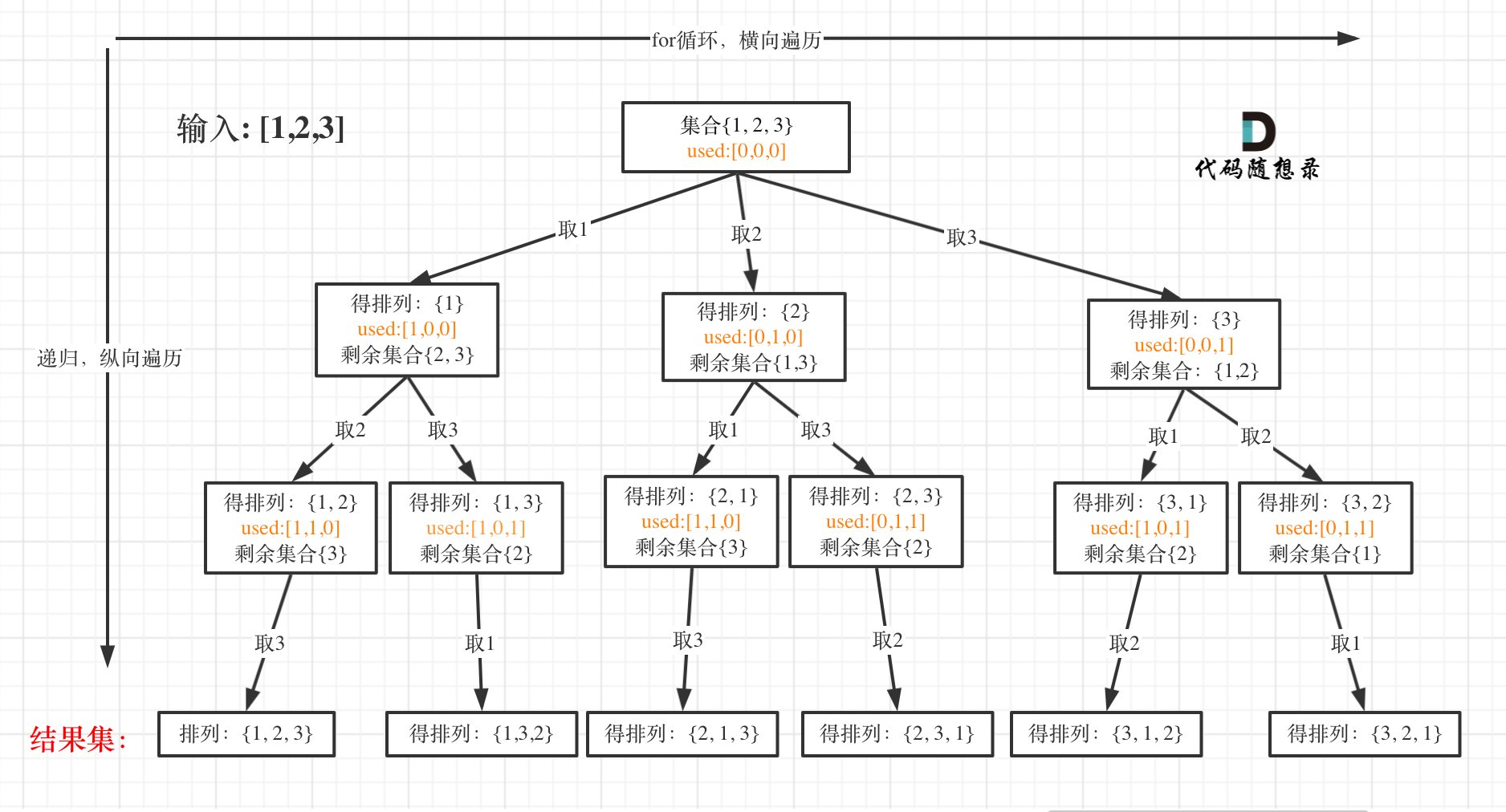
- used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次。
- 全排列labuladong 题解思路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
# 所有结果长度都为最长
def backtracing(nums, used):
nonlocal res, path
if len(path) == len(nums):
res.append(path[:])
return
for i in range(len(nums)):
if used[i]:
continue
else:
path.append(nums[i])
used[i] = True
backtracing(nums, used)
used[i] = False
path.pop()
res = []
path = []
used = [False] * len(nums)
backtracing(nums, used)
return res
全排列去重
数组去重写法:
其中
if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1])限制同一层不能遍历相同元素。如果
nums[i] == nums[i - 1]并且used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。当然也可以在树枝上去重,但不如在层上去重效率高。
set()去重参考:[[算法笔记-算法&数据结构#组合去重]]used[i]限制递归分支不能用已使用元素
1 | if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]: |
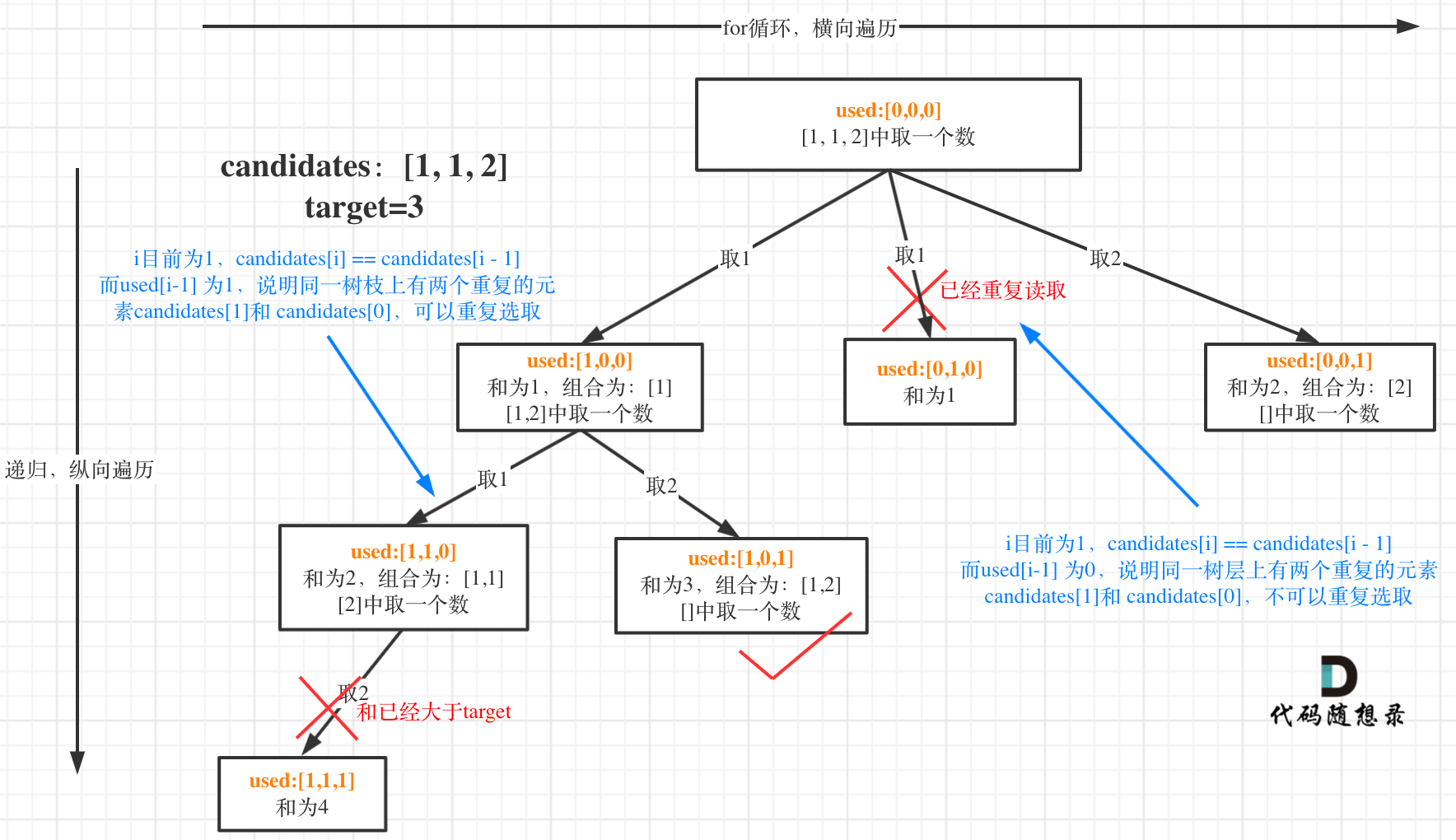
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
全排列 IIlabuladong 题解
使用数组去重1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
# 去重
def backtracing(nums, used):
if len(path) == len(nums):
res.append(path[:])
return
for i in range(len(nums)):
if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
continue
else:
path.append(nums[i])
used[i] = True
backtracing(nums, used)
used[i] = False
path.pop()
res = []
path = []
nums.sort()
used = [False] * len(nums)
backtracing(nums, used)
return res全排列 IIlabuladong 题解
使用set去重:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
# 去重
def backtracing(nums, used):
if len(path) == len(nums):
res.append(path[:])
return
cur_used = set()
for i in range(len(nums)):
if nums[i] in cur_used or used[i]:
continue
else:
path.append(nums[i])
used[i] = True
cur_used.add(nums[i])
backtracing(nums, used)
used[i] = False
path.pop()
res = []
path = []
nums.sort()
used = [False for _ in range(len(nums))]
backtracing(nums, used)
return res
棋盘问题
重新安排行程
- list的遍历过程中,必须使用pop()删除元素,remove删除的是指定元素,在循环过程中改变列表,循环的索引不会变,但对应的值发生了改变,因此要用pop(0)手动维护弹出顺序。
- 关键点在于将出发到达的关系转换成一个可递归的结构:
map<出发机场,[到达机场列表]> - 从起点寻找终点,在将终点作为起点,继续递归的过程
- 递归过程中要将使用的机场立刻删除pop(0),不然会陷入死循环
- 题目要求是字典序,因此要对
[到达机场列表]排个序 - 题目要求有一条路径就可以,因此不用遍历整棵树,设置一个bool类型返回值就可以
332. 重新安排行程1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
# 不需要遍历整棵树 找到一条符合的就可以返回了 因此使用bool返回值
def backtracing(start_point):
nonlocal path, total, tickets_dict
if len(path) == total + 1:
return True
for _ in tickets_dict[start_point]:
# 这里必须使用pop,remove删除的是指定元素,在循环过程中改变列表,循环的索引不会变,但对应的值发生了改变,因此要用pop(0)手动维护弹出顺序
end_point = tickets_dict[start_point].pop(0) # 弹出最左边航班 表示已使用
# tickets_dict[start_point].remove(end_point)
path.append(end_point)
if backtracing(end_point):
# 只要找到一个就可以返回了
return True
path.pop()
tickets_dict[start_point].append(end_point) #恢复已使用机场
# 构建 map<出发机场,[到达机场]>的数据结构
# 从出发机场开始向下递归,回溯得到结果
tickets_dict = defaultdict(list)
for ticket in tickets:
tickets_dict[ticket[0]].append(ticket[1])
# 排序
for airpoint in tickets_dict:
tickets_dict[airpoint].sort()
path = ["JFK"]
total = len(tickets)
backtracing("JFK")
return path
字典树
字典树中 父结点的孩子节点的个数等于字符集的大小。
1 | # 字典树 |
- 十叉树
对于根结点i,孩子节点的数值为 $[10i,…10i+9]$
进入子树的方式也很简单 只需要把根节点x10即可。

1 | class Solution { |
2的幂
一个数是2的幂,当且仅当n是正整数,并且n的二进制表示中只包含1个1。
那么如何计算呢,有以下两个结论。
1 | # n和n-1做与运算 如果结果为0 则n为2的幂 |
1 | # n和-n做与运算 结果为n本身 则n为2的幂 |
判断质数
1 | bool isPrime(int x) { |
Fisher-Yates 洗牌算法
1 | // 循环n次 |
公共父节点
以完全二叉树为例:
先查找较长节点的路径,再查找较短节点的路径,直到遇到形同的节点,即为公共父节点,剩下的部分为公共长度。
- 较长的路径要维护完整,即要添加第一个点
patha.add(a)
1 | class Solution: |
二叉搜索树
左子树严格小于根结点 右子树严格大于根结点
二叉搜索树的中序遍历是升序排列的,我们可以将该二叉搜索树的中序遍历的结果记录下来,得到一个升序数组。
对于普通的二叉树,可以通过先序遍历+中序遍历 或者 中序遍历+后序遍历 确定这颗二叉树。
而对于二叉搜索树,有严格的顺序关系,中序遍历是有序的,因此可以通过先序遍历或者后序遍历得到中序遍历的排序结果。
- 迭代
1 | class Solution { |
- 递归
递归性能好 空间复杂度低
1 | class Solution { |
前序遍历
1 | void findTarget(TreeNode* root, vector<int> &ans) { |
中序遍历
1 | void inorder(TreeNode *node, vector<int> &res) { |
二叉树序列化
二叉搜索树
1 | /** |
贪心
- K 次取反后最大化的数组和
1 | class Solution { |
快速乘
快速幂 使用迭代实现
注意 转成 long long 不然负数会溢出 int
1 | class Solution { |
闰年
计算闰年的简单方法
1 | year-(最近的上一个闰年+1)/4 |
前缀和
比如对于字符串s = "||**||**|*",通过计算前缀和方式就可以计算出该位置之前有多少个”*“,通过区间相减很容易得出范围内”*“的数量。
1 | int n = s.length(); |
线段树
数组分段
- 数组分块大小:
int n = sqrt(数组.size())
线段树 segmentTree 是一个二叉树,每个结点保存数组 nums 在区间 $[s,e]$ 的最小值、最大值或者总和等信息。
时间复杂度:O(n)
空间复杂度:O(n) n为数组长度
线段树的所有操作复杂度为 O(logn),
- 经验
这是一道很经典的题目,通常还能拓展出一大类问题。
针对不同的题目,我们有不同的方案可以选择(假设我们有一个数组):
数组不变,求区间和:「前缀和」、「树状数组」、「线段树」
多次修改某个数(单点),求区间和:「树状数组」、「线段树」
多次修改某个区间,输出最终结果:「差分」
多次修改某个区间,求区间和:「线段树」、「树状数组」(看修改区间范围大小)
多次将某个区间变成同一个数,求区间和:「线段树」、「树状数组」(看修改区间范围大小)
- 创建线段树 数组实现
线段树可以用树也可以用数组(堆式存储)来实现。对于数组实现,假设根结点的下标为 0,如果一个结点在数组的下标为 $node$,那么它的左子结点下标为 $node×2+1$,右子结点下标为 $node×2+2$。
1 | void build(int node, int s, int e, vector<int> &nums) { |
树状数组
树状数组下标要从1开始
lowBit
非负整数n在二进制表示下最低位1及其后面的0构成的数值
寻找最后一位11
2
3int lowBit(int x) {
return x & -x;// -x 表示x 取反加1
}
将最后一位1变成01
x & (x-1)
模版:
1 | vector<int> tree; |
树的直径


矩阵切分
对矩阵来说(0,0)表示左上角的起点,将矩阵切分只需要给定左上角坐标和需要切分的长度即可。
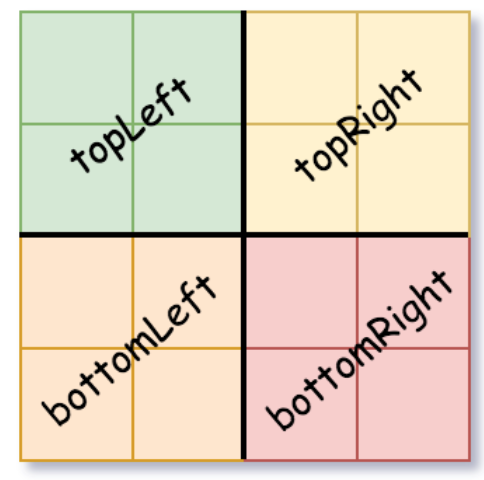
1 | dfs(grid, x, y, len/2),//左上 |
三角形面积
顶点: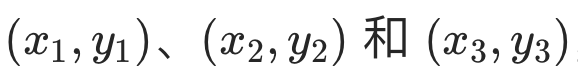
面积公式:
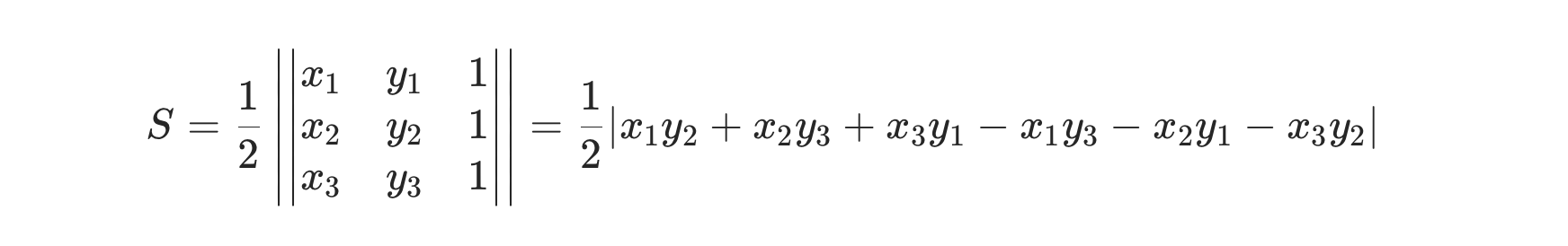
代码:
1 | // 已知三个顶点的面积公式 |