使用sklearn进行线性回归和二次回归的比较程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#coding=utf-8
"""
#演示内容：二次回归和线性回归的拟合效果的对比
"""
print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"/System/Library/Fonts/STHeiti Medium.ttc", size=20) 

def runplt():
    plt.figure()# 定义figure
    plt.title(u'披萨的价格和直径',fontproperties=font_set)
    plt.xlabel(u'直径（inch）',fontproperties=font_set)
    plt.ylabel(u'价格（美元）',fontproperties=font_set)
    plt.axis([0, 25, 0, 25])
    plt.grid(True)
    return plt

#演示内容：二次回归和线性回归的拟合效果的对比

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#训练集和测试集数据
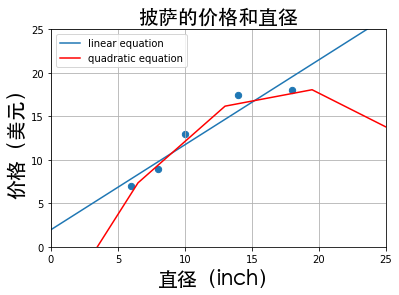
X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[7], [9], [11], [15]]
y_test = [[8], [12], [15], [18]]

#画出横纵坐标以及若干散点图
plt1 = runplt()
plt1.scatter(X_train, y_train,s=40)

#给出一些点，并画出线性回归的曲线
xx = np.linspace(0, 26, 5)
regressor = LinearRegression()
regressor.fit(X_train, y_train)
yy = regressor.predict(xx.reshape(xx.shape[0], 1))

plt.plot(xx, yy, label="linear equation")

#多项式回归（本例中为二次回归）
#首先生成多项式特征
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)

regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)

#numpy.reshape（重塑）给数组一个新的形状而不改变其数据。在指定的间隔内返回均匀间隔的数字
#给出一些点，并画出线性回归的曲线
xx = np.linspace(0, 26, 5)
print (xx.shape)
print (xx.shape[0])
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
print (xx.reshape(xx.shape[0], 1).shape)

plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-',label="quadratic equation")
plt.legend(loc='upper left')
plt.show()

X_test_quadratic = quadratic_featurizer.transform(X_test)

# 计算R^2得分 得分越高越好
print('linear equation  r-squared', regressor.score(X_test, y_test))
print('quadratic equation r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
(5,)
5
(5, 1)

output_2_1

linear equation  r-squared 0.8283656795834485
quadratic equation r-squared 0.9785451046983036