A Simple and Effective Model for Answering Multi-span Questions

论文：EMNLP20-A Simple and Effective Model for Answering Multi-span Questions

代码：https://github.com/eladsegal/tag-based-multi-span-extraction

multi-span architecture (TASE: TAg-based Span Extraction)

traditional single-span extraction (SSE)

任务

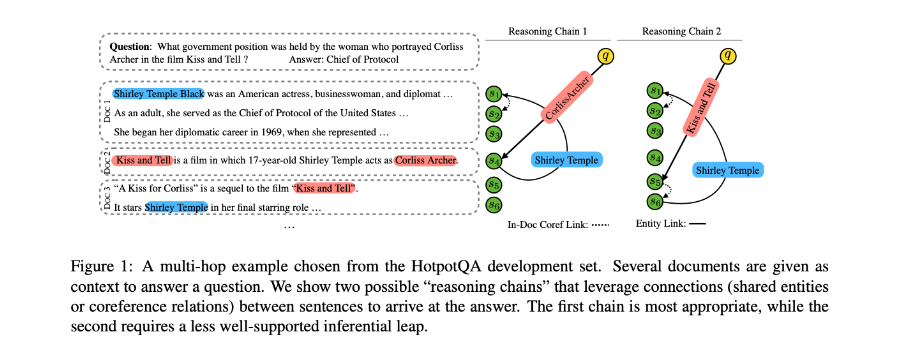
传统的阅读理解模型将问题的答案限制在单个跨度，对于答案处于多跨度的问题会有限制，本文提出了一个简单的体系结构，通过将任务转换为序列标记问题来回答多跨度问题，为每个输入token预测是否应该将其作为输出的一部分。

阅读理解(RC)任务：

在给定一个问题和上下文的情况下提供答案。

方法（模型）

Single-span Model

question-context-answer triplets $(qi, c_i, a_i)^N{i=1}$

目标：学习一个函数将一个question-context对映射到answer。

将question and context编码：

$h = Encoder([q, c])$

$h$是所有输入token的上下文表示序列:

$h = (h_1, . . . , h_m)$

前馈网络:

$p_{start}^ i = softmax (f_{start}(h_1), . . . , f_{start}(h_m))_i$ $p_{end}^ i = softmax (f_{end}(h_1), . . . , f_{end}(h_m))_i$

通过$f{start}(hi) and f{end}(hi)$计算每个token的得分，再通过softmax得到概率分布。

提取答案范围：

$(s, e) = \underset {s \le e} {arg max} \ p_s^{start} p_e^{end}$

Multi-span Model

Span Extraction as Sequence Tagging

与Single-span Model相同的是：使用相同的上下文表示$h$

不同的是：不是预测开始和结束概率，而是为每个标记在一组标签上输出概率分布。

two tagging schemes：

BIO

B：表示输出范围的第一个标记

I：表示范围中的后续标记

O：表示不属于输出范围的标记
IO

I：单词被标记为答案的一部分

O：单词未被标记为答案的一部分

本文选择较为简单的IO

这里给一个例子：

第i个token的标签的概率：

$p_i= softmax(f(h_i))$

Training

给定的答案跨度在输入中多次出现的情况：

input：“X Y Z Y Z”

answer span：{“X”, “Z”},

taggings：B O B O B, B O B O O, and B O O O B.

X必然会出现

Y必然不会出现

Z至少出现1次

在这种情况下不能明确确定基本事实BIO。

为了处理这种情况，列举了所有可能出现的标签组合：

$possibly-correct taggings, \tau$

通过最大化所有可能的正确标记的边界概率来训练模型

$\log\ p(\tau | h) = log \sum_{T ∈ \tau}(\Pi^m_{i=1}(p_i[T_i]))$

$p_i[T_i]$是token i拥有标签$T_i$的概率。

当p为1是损失最小。

Decoding Spans from a Tagging

$\hat{T} = \underset{T∈\nu}{arg\max} (\Pi^m_{i=1}(p_i[T_i]))$

$\hat{T}$：最有可能的标记

$\nu$：所有有效标记的集合

对于IO标签，所有标签均有效，并且通过独立预测每个token中概率最高的标签来实现最大化。

由于答案跨度在RC任务中从不相邻，因此IO标记通过选择所有以I连续标记的最大跨度来生成一组跨度。

“Multi-Head” Models

一些RC数据集包含的一些问题，其输出不一定是跨度的，例如：通过算术运算获取答案。

对此一些模型使用了multi-head architecture

$p_z(a | q, c) = p_z(a | h)$

每个head z是一个小模块，将上下文表示h作为输入并计算答案的概率分布。

为了确定哪个问题需要使用哪个头，需要训练一个附加模型：

$p_{head}(z | q, c) = p_{head}(z | h)$

答案的概率分布：

$p(a | q, c) = \sum_z p_{head}(z | q, c) · p_z(a | q, c)$

数据集

DROP

DROP’s leaderboard：https://leaderboard.allenai.org/drop/submissions/public
QUOREF

性能水平

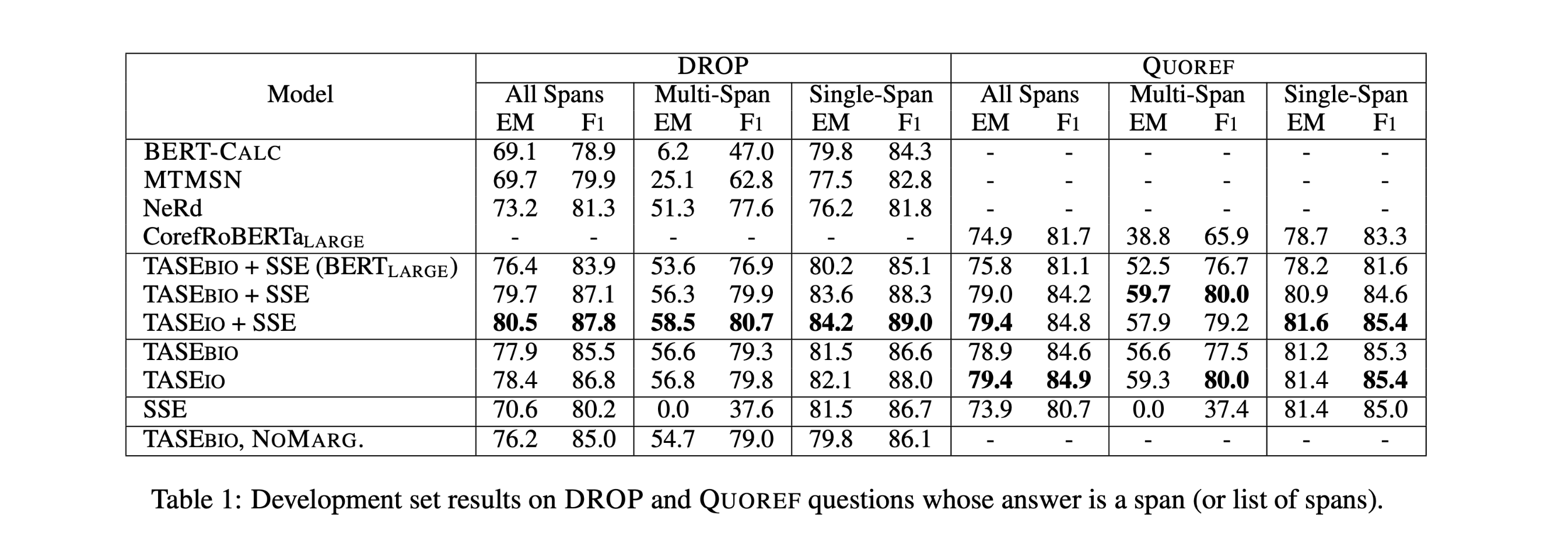
模型比较：

在DROP上:

使用$BERT{LARGE}$作为encoder的$TASE{BIO}+SSE (BERT{LARGE})$超越所有处理multi-span questions的模型。相比$BERT-C{ALC}$和$MTMSN$效果较为显著。

在QUOREF上:

处理multi-span questions是性能远超$CorefRoBERTa_{LARGE}$ 20个百分点。
跨度提取架构比较

在DROP和QUOREF中，用多跨度提取替换单跨度提取可以显著改善多跨度问题的性能，而单跨度问题的性能较之前变化不大。这表明多跨度架构本身可以用作通用跨度提取方法。
tagging方案的效果比较

BIO和IO方案，结果非常相似。IO略占优势。