1. 知识图谱(KG)

  • 由实体(节点)和关系(不同类型的边)组成的多关系图。
  • 每条边都表示为形式(头实体、关系、尾实体)的三个部分，也称为事实

1.1 问题

  • 这类三元组的底层符号特性通常使KGs很难操作

1.2 解决：

  • 提出了一种新的研究方向——知识图谱嵌入。

1.3 关键思想

  • 嵌入KG的组件，包括将实体和关系转化为连续的向量空间，从而简化操作，同时保留KG的原有的结构。

2. 融合事实信息

2.1 平移距离模型

  • 平移距离模型利用了基于距离的评分函数，通过两个实体之间的距离对事实的合理性进行度量。

img

2.1.1 TransE模型

  • 平移不变现象

  • TransE模型：将知识库中的关系看作实体间的某种平移向量。

  • 对于每个事实三元组(h,r,t)，TransE模型将实体和关系表示为同一空间中，把关系向量r看作为头实体向量h和尾实体向量t之间的平移即 $h+r≈t$。

  • 可以将r,看作从h到t的翻译

  • 知识库中的实体关系类型可分为 一对一 、一对多 、 多对一 、多对多4 种类型，而复杂关系主要指的是 一对多 、 多对一 、多对多的 3 种关系类型。

    优点
    • TransE模型的参数较少，计算的复杂度显著降低，并且在大规模稀疏知识库上也同样具有较好的性能与可扩展性。
    缺点
    • TransE模型不能用在处理复杂关系上。

2.1.2 TransH模型

  • 为了解决TransE模型在处理一对多 、 多对一 、多对多复杂关系时的局限性。
  • TransH模型提出让一个实体在不同的关系下拥有不同的表示。
  • 对于关系r，TransH模型同时使用平移向量r和超平面的法向量w_r来表示它。对于一个三元组(h, r, t) , TransH首先将头实体向量h和尾实体向量r，沿法线wr，影到关系r对应的超平面上，用h⊥和t⊥表示如下：

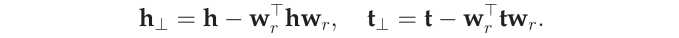
  • TransH 使不同的实体在不同的关系下拥有了不同的表示形式，但由于实体向量被投影到了关系的语义空间中，故它们具有相同的维度

    缺点：
    • 虽然TransH模型使每个实体在不同关系下拥有了不同的表示，它仍然假设实体和关系处于相同的语义空间中，这一定程度上限制了TransH的表示能力。

2.1.3 TransR模型

  • TransR模型认为，一个实体是多种属性的综合体，不同关系关注实体的不同属性。
  • 不同的关系拥有不同的语义空间。
  • 对于每一个关系r，TransR定义投影矩阵Mr，将实体向量从实体空间投影到关系r的子空间，用h⊥和t⊥表示如下：

  • 然后使 $h⊥+r≈t⊥$

    缺点：

    • 在同一个关系下：头、尾实体共享相同的投影矩阵。然而，一个关系的头、尾实体的类型或属性可能差异巨大。例如，对于三元组(美国，总统，奥巴马)，美国和奥巴马的类型完全不同，一个是国家，一个是人物。

    • 从实体空间到关系空间的投影是实体和关系之间的交互过程，因此TransR让投影矩阵仅与关系有关是不合理的。

    • 与TransE和TransH相比，TransR由于引入了空间投影，使得TransR模型参数急剧增加，计算复杂度大大提高。

2.1.4 TransD模型

  • 给定三元组(h, r, t) , TransD模型设置了2个分别将头实体和尾实体投影到关系空间的投影矩阵Mr1和Mr2。具体定义如下:

img

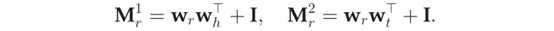
  • 尾实体用h⊥和t⊥表示如下：

img

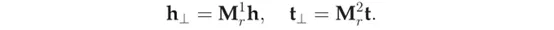
2.1.5 TranSparse模型

  • TranSparse是通过在投影矩阵上强化稀疏性来简化TransR的工作。它有两个版本：TranSparse (共享)和TranSparse (单独)。
  • TranSparse (共享)对每个关系r使用相同的稀疏投影矩阵$M_r(theta_r)$ 即：

img

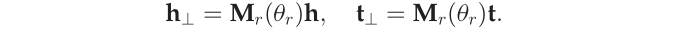
  • TranSparse (单独)对于头实体和尾实体分别使用2个不同的投影矩阵$M_r1(theta_r1$)和$M_r2(theta_r2)$。

img

  • 这里的$theta_r$、$theta_r1$和$theta_r2$表示这些投影矩阵的稀疏度。

    优点：
    • TransSparse模型通过引入稀疏投影矩阵，TransSparse模型减少了参数个数。

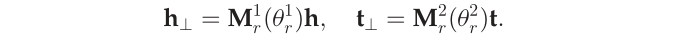
2.1.6 TransM模型

  • 除了允许实体在涉及不同关系时具有不同的嵌入之外，提高TransE模型性能可以从降低h+r≈t的要求研究开始。TransM模型将为每个事实（h,r,t）分配特定的关系权重theta_r。
  • 通过对一对多、多对一和多对多分配较小的权重，TransM模型使得t在上述的复杂关系中离h+r更远。

2.1.7 ManifoldE模型

  • ManifoldE模型对于每个事实三元组$（h,r,t）$将$h+r≈t$转换为(h+r-t)的L2范式约等于theta_r的平方。
  • ManifoldE把t近似地位于流形体上，即一个以h+r为中心半径为theta_r的超球体，而不是接近h+r的精确点。

2.1.8 TransF模型

  • TransF只需要t与h+r位于同一个方向，同时h与t-r也位于同一个方向。

2.1.9 TransA模型

  • TransA模型为每个关系r引入一个对称的非负矩阵Mr，并使用自适应马氏距离定义评分函数。

  • 通过学习距离度量Mr, TransA在处理复杂关系时更加灵活。

    问题：
    • 评分函数只采用L1或L2距离，灵活性不够。
    • 评分函数过于简单，实体和关系向量的每一维等同考虑。
    解决
    • 提出TransA模型，将评分函数中的距离度量改用马氏距离，并为每一维学习不同的权重。
    示例
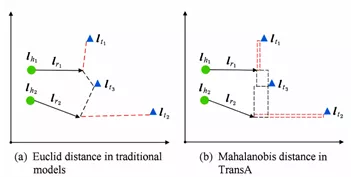
    • 如下图所示，$( h_1, r_1, t_1)$和$(h_2,r_2,t_2)$两个合法的事实三元组，t3是错误的尾实体。如果使用欧氏距离，如图(a)所示，错误的实体t3会被预测出来。而如图(b)所示，TransA模型通过对向量不同维度进行加权，正确的实体由于在x轴或者y轴上距离较近，从而能够被正确预测。

    img

2.2 高斯嵌入模型

2.2.1 KG2E模型

  • 知识库中的关系和实体的语义本身具有不确定性，而过去模型中都忽略这个因素。
  • KG2E使用高斯分布来表示实体和关系。
  • 其中高斯分布的均值表示的是实体或关系在语义空间中的中心位置，而高斯分布的协方差则表示该实体或关系的不确定度。

img

每个圆圈代表不同实体与关系的表示，它们分别与”比尔·克林顿”构成三元组，其中圆圈大小表示的是不同实体或关系的不确定度，可以看到”国籍”的不确定度远远大于其他关系。

TransG模型

  • TransG也是对高斯分布的实体进行了建模。

img

  • TransG提出使用高斯混合模型描述头、尾实体之间的关系。该模型认为，一个关系会对应多种语义，每种语义用一个高斯分布来刻画。

img

  • 传统模型和TransG模型比较

img

其中三角形表示正确的尾实体，圆形表示错误的尾实体。图(a)中为传统模型示例，由于将关系r的所有语义混为一谈，导致错误的实体无法被区分开。而图(b)所示，TransG模型通过考虑关系r的不同语义，形成多个高斯分布，就能够区分出正确和错误实体。

3 语义匹配模型

  • 使用基于相似度的评分函数。
  • 通过匹配实体的潜在语义和向量空间表示中包含的关系来度量事实的可信性。

3.1 RESCAL模型及其扩展

img

3.1.1 RESCAL模型

  • RESCAL(又称双线性模型)通过使用一个向量表示每个实体来获得它的潜在语义。
  • 每个关系都表示为一个矩阵，该矩阵对潜在因素之间的成对交互作用进行了建模。它把事实$（h,r,t）$评分函数定义为一个双线性函数。

3.1.2 DistMult模型

  • DistMult通过将Mr限制为对角矩阵来简化RESCAL。(Mr关系矩阵)
  • 评分函数只捕获沿同一维度的h和t分量之间的成对交互作用(参阅图5 b)，并将每一个关系的参数数量减少至O(d)。
  • 然而，因为对于任意的h和t，$h^Tdiag(r)t = t^Tdiag(r)h$都是成立的，这种过度简化的模型只能处理对称的关系，这显然对于一般的KGs是不能完全适用的。

3.1.3 HolE模型

  • HolE将RESCAL的表达能力与DistMult的效率和简单性相结合。
  • 把实体和关系都表示为$R_d$中的向量。给定一个事实$(h,r,t)$，首先使用循环相关操作将实体表示形式组成$h*t∈R$。

img

  • 然后将组合向量与关系表示形式匹配，以对事实进行评分。

img

  • 循环相关对成对的相互作用进行压缩。因此，HolE对每个关系只需要$O(d)$参数，这比RESCAL更有效。与此同时，因为循环相关是不符合交换律的，即$ht$不等于$th$。所以HolE能够像RESCAL那样对不对称关系进行建模。

3.1.4 ComplEx模型

  • ComplEx通过引入复值嵌入来扩展DistMult，以便更好地对非对称关系进行建模。
  • 在ComplEx中，实体和关系嵌入h，r, t不再存在于实空间中，而是存在于复空间中。

img

评分函数

这个评分函数不再是对称的，来自非对称关系的事实可以根据涉及实体的顺序得到不同的分数。

3.1.5 ANALOGY模型

  • ANALOGY 扩展了RESCAL，从而进一步对实体和关系的类比属性进行建模。
  • 它遵循RESCAL并使用双线性评分函数。
  • 尽管ANALOGY表示关系为矩阵，这些矩阵可以同时对角化成一组稀疏的准对角矩阵，由每个只有$O(d)$自由参数。

3.2 基于神经网络匹配

3.2.1 语义匹配能量模型(SME)

  • SME采用神经网络结构进行语义匹配。
  • 给定一个事实三元组$（h,r,t）$，它首先将实体和关系投影到输入层中的嵌入向量。然后，将关系r与头实体h组合得到$g_u(h,r)$，并与尾实体t组合，得到隐藏层中的$g_v(t,r)$。则该事实的分数最终由它们的点积定义为匹配的$g_u$和$g_v$。

  • SME有两个版本：线性版本和双线性版本。

3.2.2 神经张量网络模型(NTN)

  • NTN是另外一种神经网络结构，给定一个事实，它首先将实体投影到输入层中的嵌入向量。然后，将这两个实体h,t由关系特有的张量$M_r$(以及其他参数)组合，并映射到一个非线性隐藏层。最后，一个特定于关系的线性输出层给出了评分。

img

  • 尽管NTN是迄今为止最具表达能力的模型，但是，由于它的每个关系的需要O(d^2*k)个参数，并且不能简单有效地处理大型的KGs。

3.2.3 多层感知机(MLP)

  • MLP是一种更简单的方法，在这种方法中，每个关系(以及实体)都是由一个向量组合而成的。
  • 给定一个事实$（h,r,t）$将嵌入向量h、r和t连接在输入层中，并映射到非线性的隐藏层。然后由线性输出层生成分数。

img

其中$M_1、M_2、M_3$是第一层的权重，w是第二层的权重，这些都是在不同的关系中共享的。

3.2.4 神经关联模型(NAM)

  • NAM使用“深度”架构进行语义匹配，给定一个事实，它首先将头实体的嵌入向量和输入层中的关系连接起来，从而给出$z_0=[h,r]$。然后输入$z_0$输入到一个由L个线性隐层组成的深神经网络中。

img

其中$M(l)$和b(l)分别表示第l层的权重矩阵和偏差。

  • 在前馈过程之后，通过匹配最后一个隐藏层的输出和尾实体的嵌入向量来给出分数。

img

4 融合附加信息

  • 目前介绍的方法仅使用KG中观察到的事实来执行嵌入任务。事实上，可以合并许多附加信息来进一步改进任务，例如实体类型、关系路径、文本描述以及逻辑规则。

4.1 实体类型

  • 即实体所属的语义类别。
  • 实体类型也可以作为不同关系的头部和尾部位置的约束，例如关系DirectorOf的头实体的类型应该是人，尾实体的类型应该是电影作品。

4.1.1语义平滑嵌入(SSE)模型

  • 它要求相同类型的实体在嵌入空间中彼此邻近。

  • SSE采用两种流形学习算法，即拉普拉斯特征映射和局部线性嵌入来对这种光滑性假设进行建模。

    拉普拉斯特征映射：要求一个实体和同一类别中的每一个其他实体邻近。

    局部线性嵌入：一个实体视为其最近邻居的线性组合，即同一类别内的实体。

  • SSE的一个主要限制是它假设实体的语义范畴是无层次的，每个实体完全属于一个类别。显然，在典型的现实世界中，情况并非如此。

4.1.2 TKRL模型

  • 它可以处理分层实体类别和多个类别标签。
  • TKRL是一个具有特定类型实体投影的平移距离模型。给定一个事实$(h,r,t)$，它首先用特定类型的投影矩阵预测h和t，然后将r建模为两个投影实体之间的平移。

img

评分函数

其中$M_rh$和$M_rt$是h和t的投影矩阵，为了处理多个类别标签，$M_r$h表示为所有可能的类型矩阵的加权和。

  • 虽然TKRL在链路预测和三元组分类等下游任务中取得了较好的性能，但由于它将每个类别与特定的投影矩阵相关联，因此具有较高的空间复杂度。