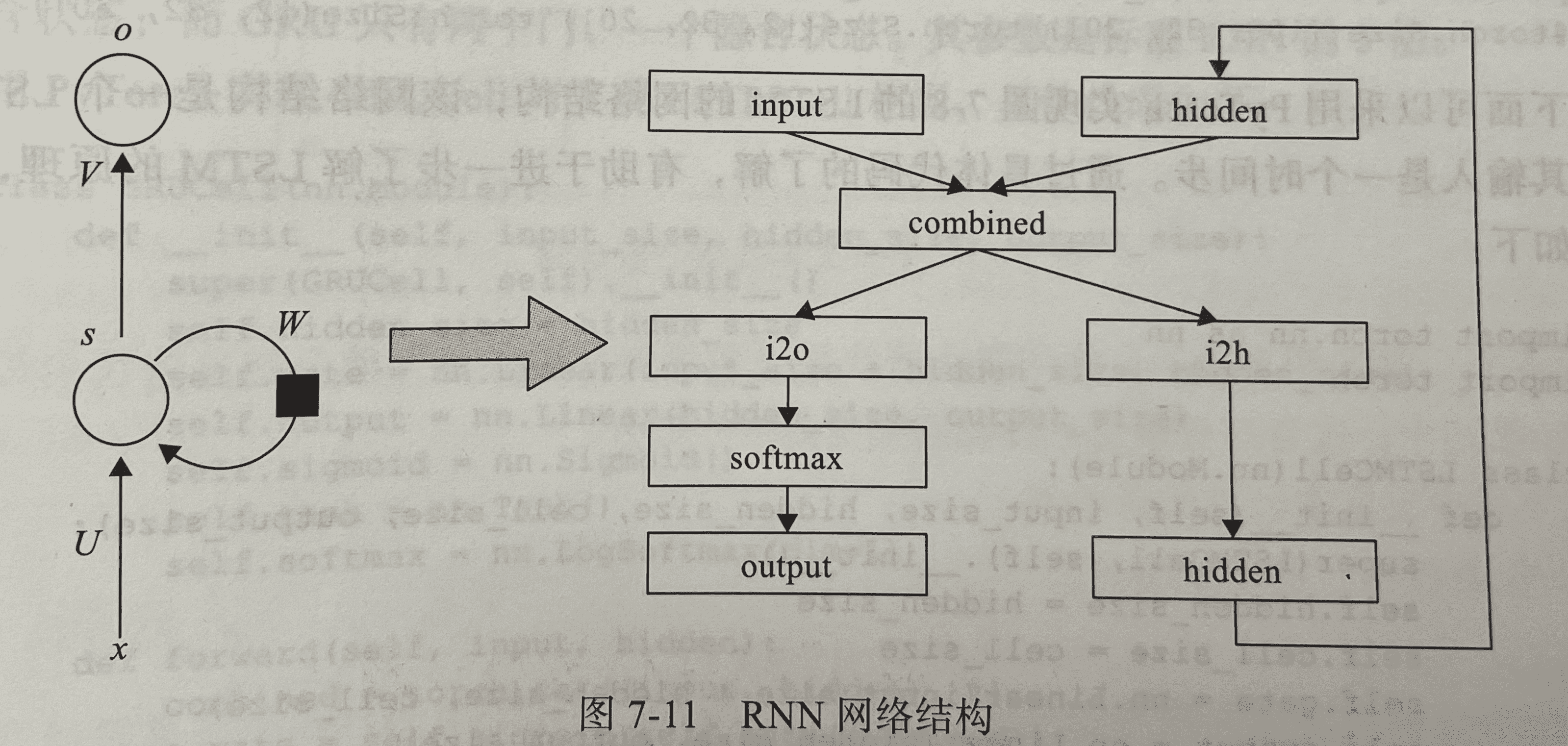
RNN循环神经网络

序列数据：与先后顺序有关的数据。
对于序列数据，可以使用循环神经网络。

$H_t=ϕ(X_tW_{xh}+H_{t−1}W_{hh}+b_h)$ $O_t=H_tW_{hq}+b_q$

$X_t∈R^{n×d}$是序列中时间步$t$小批量输入。

$H_t∈R^{n×h}$是该时间步的隐藏变量。

隐藏层的权重$W{xh}∈R^{d×h}$、$W{hh}∈R^{h×h}$和偏差 $b_h∈R^{1×h}$

输出层的权重$W_{hq}∈R^{h×q}$和偏差$b_q∈R^{1×q}$

时间步$t$的隐藏变量的计算由当前时间步的输入和上一时间步的隐藏变量共同决定。

其中：$XtW{xh}+H{t−1}W{hh}$可以写成矩阵$[Xt,H{t−1}]^T$与$[W{xh},W{hh}]$连接后的乘积。

含隐藏状态的循环神经网络:

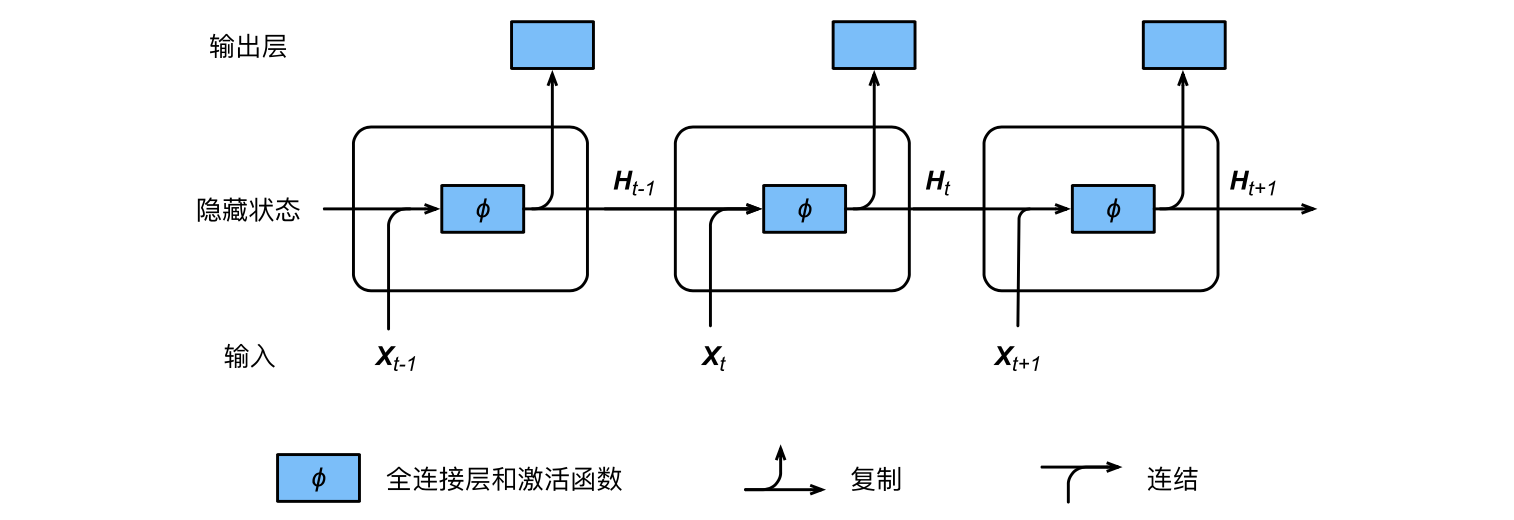
在时间步$t$，隐藏状态的计算可以看成是将输入$Xt$和前一时间步隐藏状态$H{t−1}$连结后输入一个激活函数为$ϕ$的全连接层。

该全连接层的输出就是当前时间步的隐藏状态$Ht$ ，且模型参数为Wxh与$W{hh}$ 的连结，偏差为$b_h$。

当前时间步$t$的隐藏状态$Ht$将参与下一个时间步$t+1$的隐藏状态$H{t+1}$ 的计算，并输入到当前时间步的全连接输出层。

前面说到$XtW{xh}+H{t−1}W{hh}$等价于矩阵$[Xt,H{t−1}]^T$与$[W{xh},W{hh}]$连接后的乘积，我们来验证一下：

构造矩阵：

import torch

X, W_xh = torch.randn(3, 1), torch.randn(1, 4)
H, W_hh = torch.randn(3, 4), torch.randn(4, 4)

代入公式：

1	torch.matmul(X, W_xh) + torch.matmul(H, W_hh)

输出：

1
2
3

tensor([[ 1.2453, -0.3466,  1.1116, -2.0741],
        [ 7.5939,  0.3180,  0.7647,  2.4541],
        [ 2.9573, -0.0598,  0.1762,  0.1142]])

矩阵连接之后：

dim=1：列拼接

dim=0：行拼接

1	torch.matmul(torch.cat((X, H), dim=1), torch.cat((W_xh, W_hh), dim=0))

输出：

1
2
3

tensor([[ 1.2453, -0.3466,  1.1116, -2.0741],
        [ 7.5939,  0.3180,  0.7647,  2.4541],
        [ 2.9573, -0.0598,  0.1762,  0.1142]])