GCN

GCN：图卷积网络

SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS：基于图卷积网络的半监督分类

任务

  • 在图结构数据中，一部节点已知标签，剩下的节点标签未知，使用已知标签的节点训练卷积神经网络，使用网络模型对无标签的节点进行分类。

方法（模型）

  • 提出了一种可扩展的基于图结构数据的半监督分类方法。
  • 分层传播规则：通过谱图卷积（spectral graph convolutions） 的局部一阶近似，来确定卷积网络结构。

$f(X,A)$

  • 使用神经网络$f(X,A)$对图的结构进行编码，对所有带标签的节点进行有监督训练。

  • 避免显式地对基于图的损失函数进行正则化计算

  • 在图的邻接矩阵上调节$f (⋅)$ ，允许模型从监督损失$\mathcal{L}_{0}$中分开梯度信息，使其能够学习所有节点的表示。

  • X：输入数据

    A：图邻接矩阵

FAST APPROXIMATE CONVOLUTIONS ON GRAPHS

  • 图卷积的前向传播公式：

SPECTRAL GRAPH CONVOLUTIONS

频谱图形卷积

半监督分类图卷积网络是在先前的频谱卷积网络的基础上通过局部一阶近似得到的

  • 对于一个输入信号 $x \in \mathbb{R}^N$ ，在傅里叶域中取一个$\theta \in \mathbb{R}^N$为参数的滤波器$g_{\theta} = diag(\theta)$。

    将图卷积通过傅里叶变换拓展到图的频域中。

    第一代GCN图卷积公式

    缺点：计算复杂

  • 将$g_{\theta}(\Lambda)$用切比雪夫多项式（Chebyshev）进行K阶逼近。

    改进的卷积核：

  • 将该卷积核代入图卷积的公式：

    将参数减少到了K个，并且不再需要对拉普拉斯矩阵做特征分解。

LAYER-WISE LINEAR MODEL

线性模型

  • 限制参数数量可以进一步解决过拟合并将各层的运算量最小化，使得可以通过堆叠多个GCN来获得一个更深的模型，提取特征。
  • 为解决数值不稳定性和梯度爆炸/消失，进行了再归一化。
  • 限制参数的数量以解决过度拟合问题，并最小化每层的运算数量(例如矩阵乘法)。

SEMI-SUPERVISED NODE CLASSIFICATION

半监督节点分类

  • 使用已知的数据$X$和邻接矩阵$A$来训练图卷积网络 $f(X, A)$。

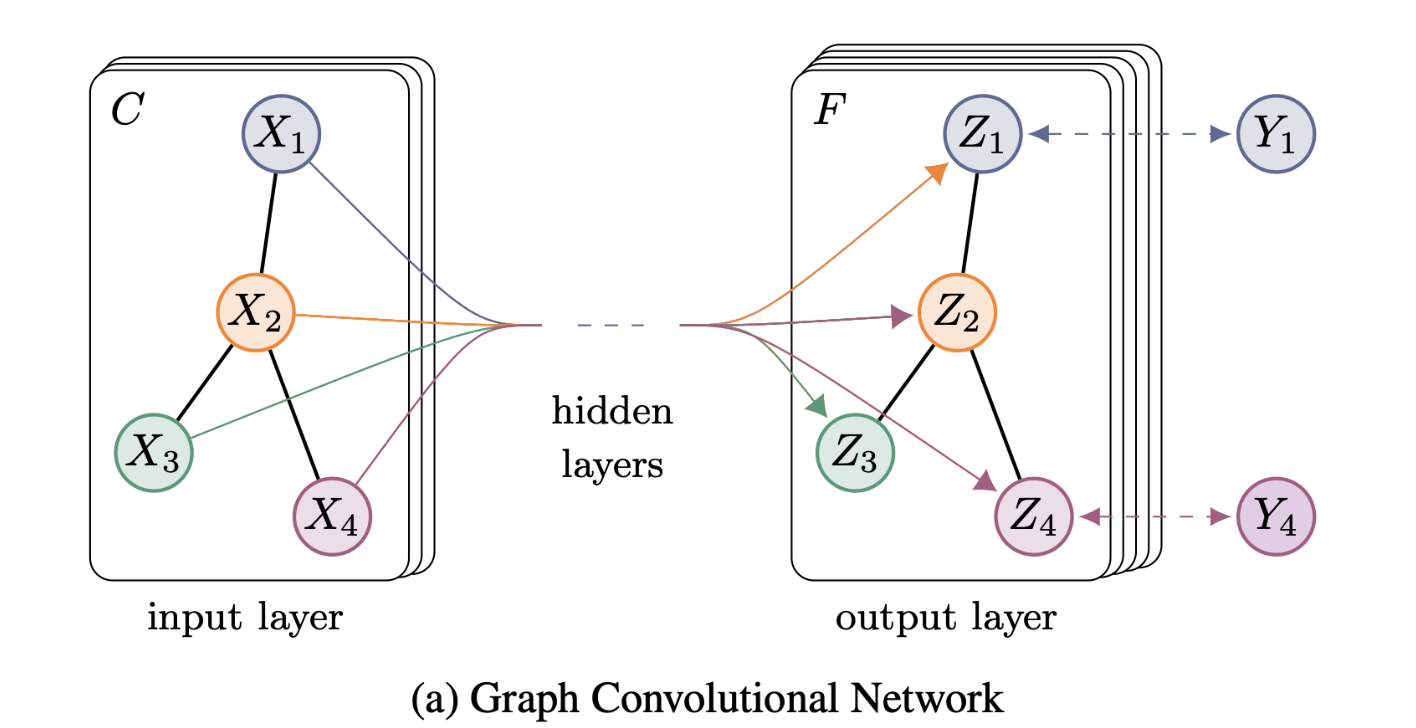
image-20201110211205798

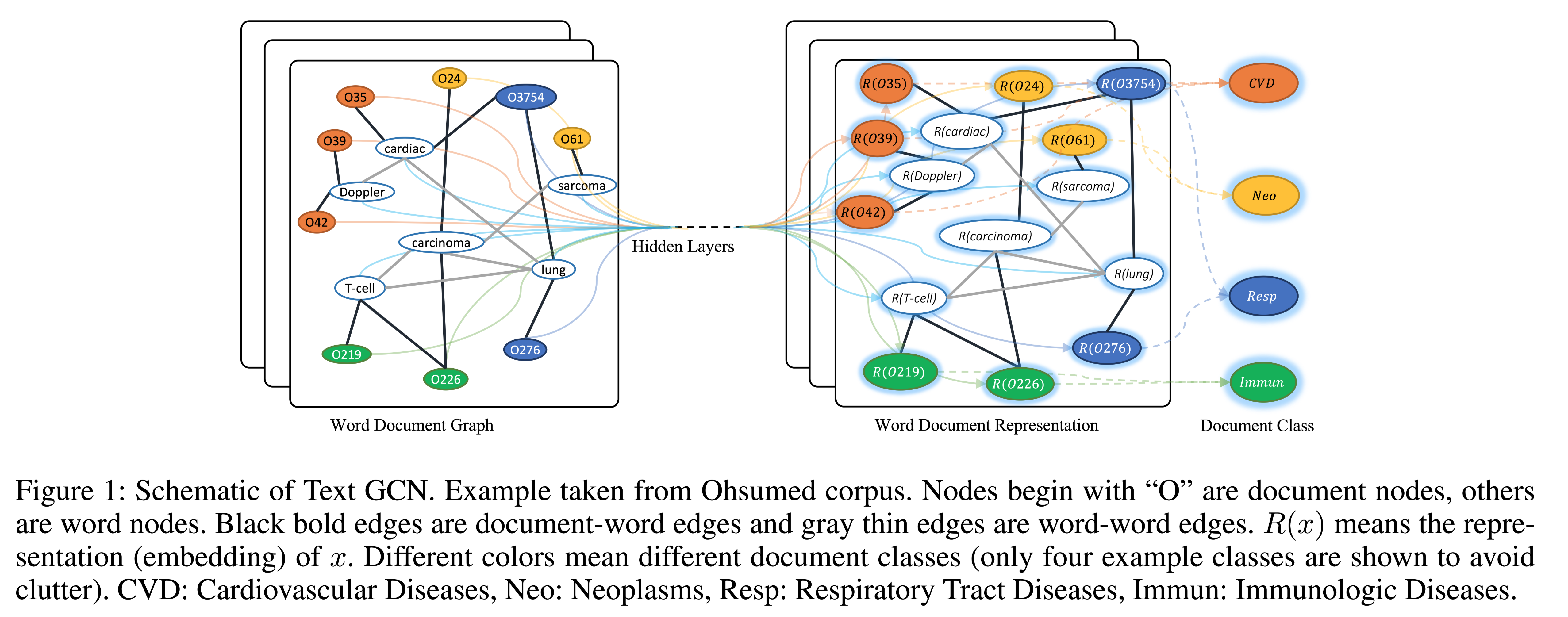
GCN网络示意图

  • 输入层拥有C个输入，中间有若干隐藏层，在输出层有F个特征映射。

  • 图的结构在层之间共享。

  • 标签用$Y_{i}$ 表示。

image-20201110211553795

两层GCN在Cora数据集上（使用了5%的标签）训练得到的隐藏层激活值的形象化表示，颜色表示文档类别。

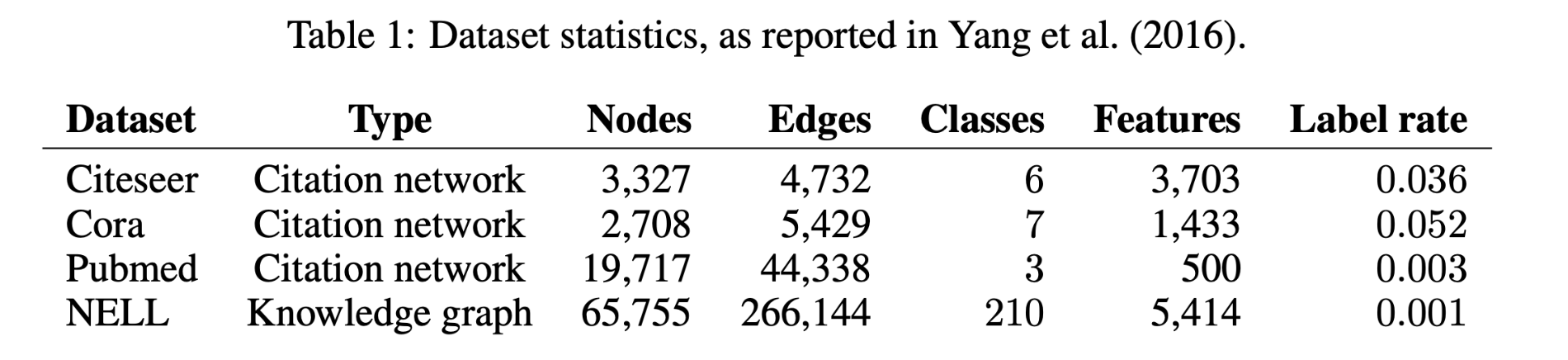
数据集

Citeseer,Cora ,Pubmed ,NELL

引文网络数据集：Citeseer,Cora,Pubmed

image-20201110211901273

性能水平

比较模型：

流形正则化(ManiReg)、半监督嵌入(SemiEmb)、标签传播(LP)、基于跳跃文法的图嵌入(DeepWalk)、迭代分类算法(ICA)、两个Logistic回归分类器。

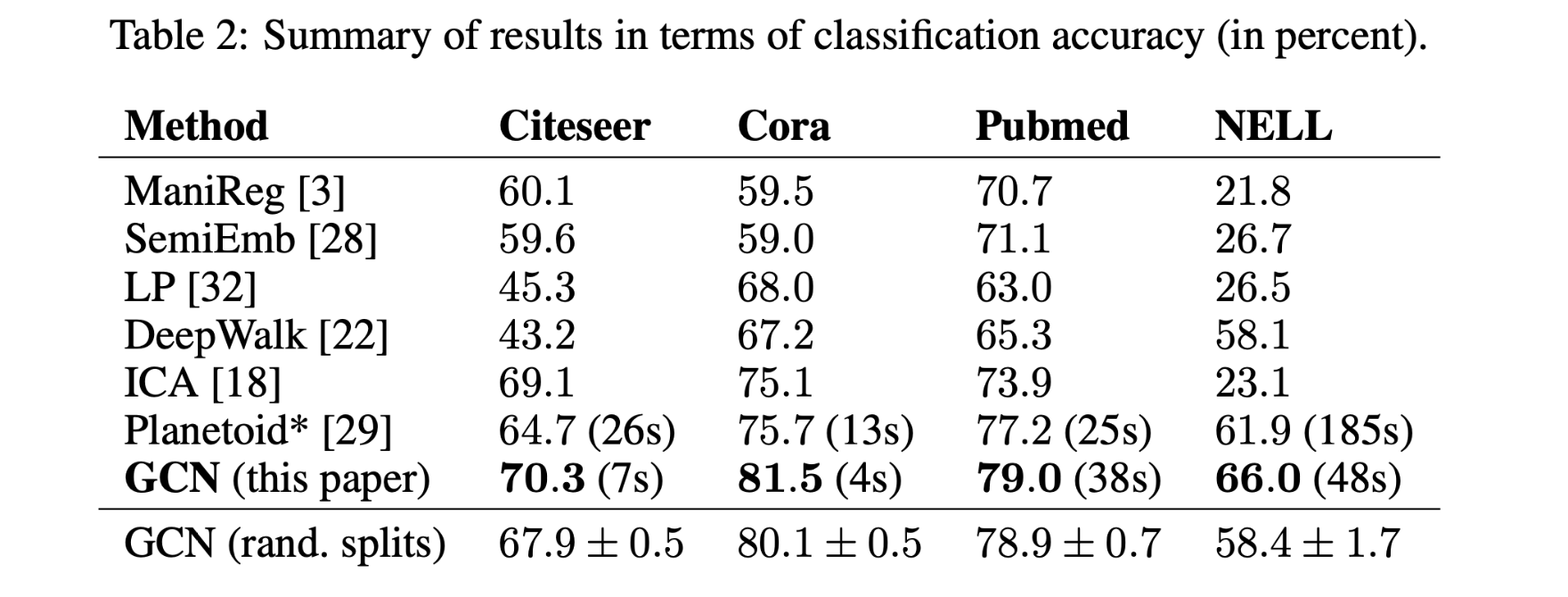
image-20201110213407738

  • GCN在四个数据集上的表现都比较突出，分类准确性较高。

  • 提出的GCN模型能够同时对图结构和节点特征进行编码，对半监督分类是有用的。

思考

有监督学习、无监督学习和半监督学习的分类

  • 监督学习是使用已知正确答案的示例来训练网络的。
  • 无监督学习适用于具有数据集但无标签的情况。
  • 半监督学习在训练阶段结合了大量未标记的数据和少量标签数据。