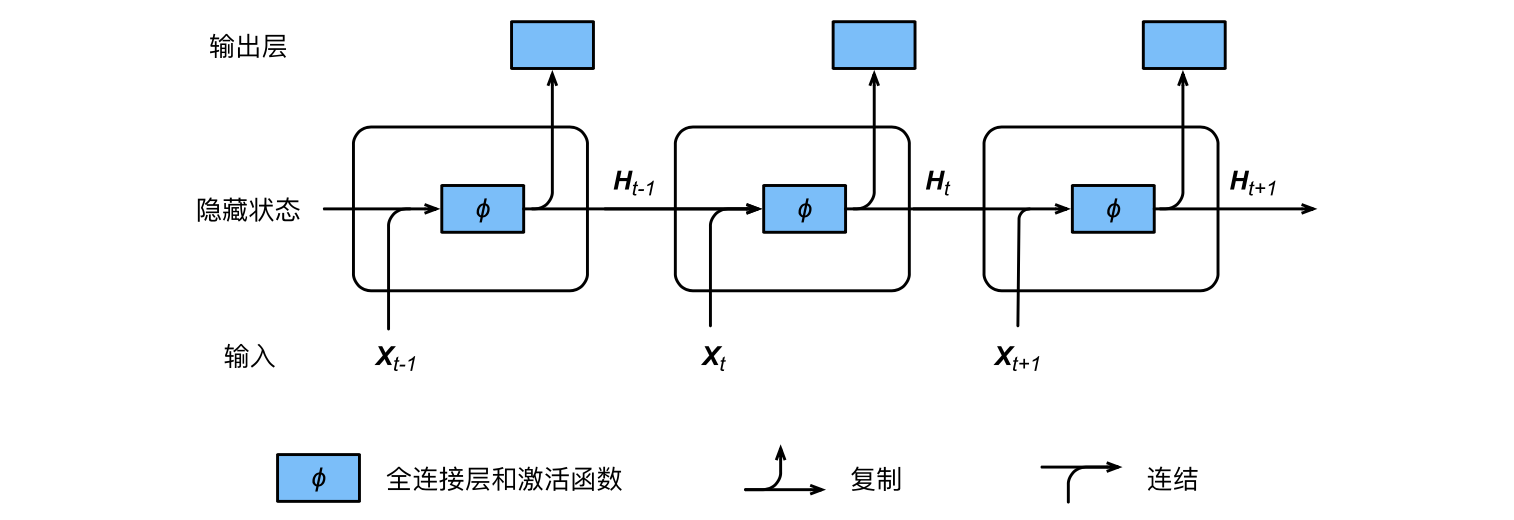
PyTorch自动求导
标量反向传播
当目标张量为标量时,backward()无需传入参数。
- 例子:假设$w,x,b$都是标量,$z=wx+b$ ,对标量$z$调用backward()方法。
自动求导的主要步骤
1 | import torch |
1.定义叶子结点,算子节点
如果需要对Tensor求导,requires_grad要设置为True。
1 | # 定义输入张量x |
False
True
2.查看叶子结点,非叶子结点的其他属性
- grad_fn:表示梯度函数
通过运算创建的Tensor(非叶子结点)会自动被赋予grad_fn属性。
叶子结点的grad_fn为None。
1 | # 查看非叶子结点y,z的requires_grad属性。 |
True
True
False
x的grad_fn属性: None
y的grad_fn属性: <MulBackward0 object at 0x7fe83935dbb0>
3.自动求导,实现梯度反向传播
非叶子节点的梯度调用backward()之后,梯度将被清空。
1 | # 基于z对张量进行反向传播,执行backward之后计算图会清空。 |
x的梯度是: None
w的梯度是: tensor([2.])
非标量反向传播
Pytorch只允许标量对张量进行求导
步骤
1.定义叶子结点,计算结点
1 | import torch |
1 | # 定义叶子张量x,形状为1x2 |
tensor([[2., 3.]], requires_grad=True)
tensor([0., 0.])
tensor([[13., 13.]], grad_fn=<CopySlices>)
2.调用backward()获取y对x的梯度
需要重复使用backward()时,retain_graph=True
1 | # 生成y1对x的梯度 |
tensor([[4., 3.],
[2., 6.]])
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 没有胡子的猫Asimok!
评论